Question

【題目】已知圓與直線相切于點(diǎn)，圓心在軸上.

（1）求圓的方程；

（2）過點(diǎn)且不與軸重合的直線與圓相交于兩點(diǎn)，為坐標(biāo)原點(diǎn)，直線分別與直線相交于兩點(diǎn)，記，的面積分別是，求的取值范圍.

Answer 1

【答案】（1）； （2）.

【解析】

（1）由題可知：設(shè)圓的方程為，根據(jù)題意可得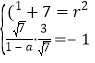，求出，即可得到圓的方程；

（2）由題意知：，

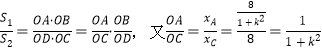設(shè)直線的斜率為，則直線的方程為，聯(lián)立可得，同理可得. 由題意知，，，因此，，同理，

所以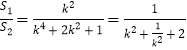，由此可求的取值范圍.

（1）由題可知：設(shè)圓的方程為，

，

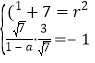解得：，

所以圓的方程為.

（2）由題意知：，

設(shè)直線的斜率為，則直線的方程為，

由，得，

解得：或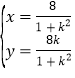，則點(diǎn)的坐標(biāo)為，

又直線的斜率為，同理可得點(diǎn)的坐標(biāo)為.

由題意知，，，

因此，.

又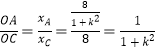，同理，，

所以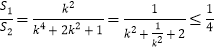，當(dāng)且僅當(dāng)時取等號.

又，所以的取值范圍是.