
���}Ŀ����֪�A![]() ���c(di��n)P������
���c(di��n)P������![]() �ϵĄ�(d��ng)�c(di��n)���^�c(di��n)P�քe��AN���о�
�ϵĄ�(d��ng)�c(di��n)���^�c(di��n)P�քe��AN���о�![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
��1����![]() �����о��ķ��̣�
�����о��ķ��̣�
��2�����о�![]() �քe��y�S���c(di��n)
�քe��y�S���c(di��n)![]() ���c(di��n)P�ęM����(bi��o)����2����
���c(di��n)P�ęM����(bi��o)����2����![]() ����eS����Сֵ.
����eS����Сֵ.
���𰸡���1��![]() ��
��![]() ����2��
����2��![]()
��������
��1���ֳ��о���б�ʲ����ںʹ��ڃɷN��r���Y(ji��)���c(di��n)��ֱ���ľ��x��ʽ������о��ķ���.
��2���O(sh��)��![]() �c(di��n)������(bi��o)������о�
�c(di��n)������(bi��o)������о�![]() �ķ��̣����ÈA�ĵ��о��ľ��x���ڰ돽��ʽ.�����e
�ķ��̣����ÈA�ĵ��о��ľ��x���ڰ돽��ʽ.�����e![]() �ı��_(d��)ʽ�����û�������ʽ�����e����Сֵ.
�ı��_(d��)ʽ�����û�������ʽ�����e����Сֵ.
��1�����}�⣬�A![]() �ĈA�Ğ�
�ĈA�Ğ�![]() ���돽��
���돽��![]() .��?y��n)?/span>
.��?y��n)?/span>![]() �����Ԯ�(d��ng)�^
�����Ԯ�(d��ng)�^![]() �c(di��n)��ֱ��б�ʲ����ڕr(sh��)��ֱ��
�c(di��n)��ֱ��б�ʲ����ڕr(sh��)��ֱ��![]() �c�A���У������}��.��(d��ng)
�c�A���У������}��.��(d��ng)![]() �c(di��n)��ֱ��б�ʴ��ڕr(sh��)���O(sh��)�о���б�ʞ�
�c(di��n)��ֱ��б�ʴ��ڕr(sh��)���O(sh��)�о���б�ʞ�![]() ���t�о����̞�
���t�о����̞�![]() ����
����![]() .�A��
.�A��![]() ���о��ľ��x
���о��ľ��x![]() �����
�����![]() ���˕r(sh��)�о����̞�
���˕r(sh��)�о����̞�![]() .
.
�C���������о����̞�![]() ��
��![]() .
.
��2���O(sh��)![]() ���t
���t![]() ���O(sh��)
���O(sh��)![]() ���t
���t![]() ������ֱ��
������ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ����?y��n)�ֱ��
����?y��n)�ֱ��![]() �c�A
�c�A![]() ��������
��������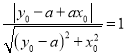 ����
����![]() .
.
ͬ������ֱ��![]() �c�A
�c�A![]() ������
������![]() .
.
����![]() �Ƿ���
�Ƿ���![]() �ăɸ������Єeʽ
�ăɸ������Єeʽ![]() ��
��![]() ���t
���t![]()
![]() .
.
����![]()
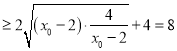 ����(d��ng)�҃H��(d��ng)
����(d��ng)�҃H��(d��ng)![]() �r(sh��)����̖(h��o)����������
�r(sh��)����̖(h��o)����������![]() ����Сֵ��
����Сֵ��![]() .
.


 ���o(j��)��ͨ���w�n��С�W(xu��)�n�r(sh��)ͬ���_(d��)��(bi��o)ϵ�д�
���o(j��)��ͨ���w�n��С�W(xu��)�n�r(sh��)ͬ���_(d��)��(bi��o)ϵ�д� ���o(j��)��ͨ��(y��u)���yϵ�д�
���o(j��)��ͨ��(y��u)���yϵ�д� �ٷW(xu��)�����I(y��)���}����ϵ�д�
�ٷW(xu��)�����I(y��)���}����ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �Ľ����c�E�A
�Ľ����c�E�A![]() �Ķ��S�L��ȣ���
�Ķ��S�L��ȣ���![]() �c
�c![]() ���L�S�L���.
���L�S�L���.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)![]() �քe��E�A
�քe��E�A![]() �����ҽ��c(di��n)������(j��ng)�^
�����ҽ��c(di��n)������(j��ng)�^![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() ���ڃɂ�(g��)��ͬ���c(di��n)
���ڃɂ�(g��)��ͬ���c(di��n)![]() �����ֱ��
�����ֱ��![]() ��б�����γɵȲ(sh��)�У���
��б�����γɵȲ(sh��)�У���![]() ����e�����ֵ.
����e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij���О��˽��ο��˔�(sh��)��׃��Ҏ(gu��)�ɣ�������η���(w��)�|(zh��)�����ռ���������2016��1����2018��12�����g�½Ӵ��ο�������λ���f�ˣ��Ĕ�(sh��)��(j��)���L����������۾��D������(j��)ԓ�۾��D�����нY(ji��)Փ�e(cu��)�`���ǣ� ��
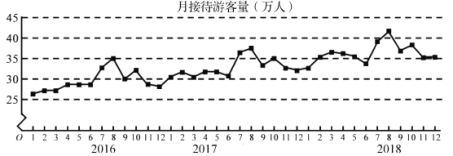
A.������½Ӵ��ο����߷��ڴ�����7��8�·�
B.��Ӵ��ο�����������
C.�½Ӵ��ο�����������
D.����1����6�µ��½Ӵ��ο�������7����12�£�����(d��ng)�Ը�С��׃�����^ƽ��(w��n)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() �^�c(di��n)
�^�c(di��n)![]() ���ҙE�A���x���ʞ�
���ҙE�A���x���ʞ�![]() ��
��
(��)��E�A![]() �ķ��̣�
�ķ��̣�
(��)б�ʞ�![]() ��ֱ��
��ֱ��![]() ���E�A
���E�A![]() ��
��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ����ֱ��
����ֱ��![]() �ϴ����c(di��n)P��ʹ��
�ϴ����c(di��n)P��ʹ��![]() ����
����![]() ��픽ǵĵ���ֱ�������Σ���ֱ��
��픽ǵĵ���ֱ�������Σ���ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() ��
��![]() .
.
��1���Дຯ��(sh��)��![]() ��
��![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2�����څ^(q��)�g![]() �ϵ����ⲻ��Ȍ�(sh��)��(sh��)
�ϵ����ⲻ��Ȍ�(sh��)��(sh��)![]() ��
��![]() ������
������![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������к���(sh��)�Ć��{(di��o)�^(q��)�g��
(1)f(x)��![]() (x��[��2,4])��
(x��[��2,4])��
(2)y��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���κ���(sh��)![]() �M��
�M��![]() ����
����![]() ��
��
![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() �O(sh��)
�O(sh��)![]() �������ڌ�(sh��)��(sh��)a��bʹ��
�������ڌ�(sh��)��(sh��)a��bʹ��![]() ����a��ȡֵ������
����a��ȡֵ������
![]() ������
������![]() ��
��![]() ����
����![]() ���������(sh��)��(sh��)t��ȡֵ������
���������(sh��)��(sh��)t��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ����֪�����F![]() �У�����
�У�����![]() �ǵ�߅�����Σ���
�ǵ�߅�����Σ���![]() ��
��![]() �քe��
�քe��![]() �����c(di��n).
�����c(di��n).

��1���C����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(ji��)�^�ס��ҡ�������Մ?w��)������P(gu��n)![]() ���Ӱ
���Ӱ![]() ��
��![]() ��
��![]() ����r.
����r.
���f���қ]�п��^�Ӱ![]() ��������
��������![]() ���Ӱ�҂�?n��i)���(g��)�����^��
���Ӱ�҂�?n��i)���(g��)�����^��
���f�������Ӱ����![]() ���Ӱ�҂�?n��i)�����ֻ��һ�˿��^��
���Ӱ�҂�?n��i)�����ֻ��һ�˿��^��
���f���Һͼ����Ӱ��![]() ����ͬ����
����ͬ����![]() ����ͬ.
����ͬ.
�����������f������Ԓ���t�ɴ˿��Д������Ӱ���ҿ��^�IJ���(sh��)�ǣ� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com