
【題目】在![]() (n≥2)個(gè)實(shí)數(shù)組成的n行n列的數(shù)表中,
(n≥2)個(gè)實(shí)數(shù)組成的n行n列的數(shù)表中, ![]() 表示第i行第j列的數(shù),記
表示第i行第j列的數(shù),記![]() .
. ![]() 若
若![]() {-1,0,1} (
{-1,0,1} (![]() ),且r1,r2,…,rn,c1,c2,..,cn,兩兩不等,則稱此表為“n階H表”,記
),且r1,r2,…,rn,c1,c2,..,cn,兩兩不等,則稱此表為“n階H表”,記
H={ r1,r2,…,rn,c1,c2,..,cn}.
(I)請寫出一個(gè)“2階H表”;
(II)對任意一個(gè)“n階H表”,若整數(shù)![]() ,且
,且![]() ,求證:
,求證: ![]() 為偶數(shù);
為偶數(shù);
(Ⅲ)求證:不存在“5階H表”.
【答案】(I)見解析;(II)見解析;(III)見解析.
【解析】試題分析:(I)由單一即可寫出;
(II)對任意一個(gè)“![]() 階
階![]() 表”,
表”, ![]() 表示第
表示第![]() 行所有數(shù)的和,
行所有數(shù)的和, ![]() 表示第
表示第![]() 列所有數(shù)的和
列所有數(shù)的和
(![]() ),可知
),可知![]()
![]() . 進(jìn)而得到
. 進(jìn)而得到![]()
![]()
![]()
![]() .所以
.所以![]()
![]() 為偶數(shù).
為偶數(shù).
(III)假設(shè)存在一個(gè)“![]() 階
階![]() 表”,則由(II)知
表”,則由(II)知![]() ,且
,且![]() 和
和![]() 至少有一個(gè)成立,不妨設(shè)
至少有一個(gè)成立,不妨設(shè)![]() .
.
設(shè)![]() ,則
,則![]() ,于是
,于是![]() ,因而可設(shè)
,因而可設(shè)![]() ,
,
![]() ,
, ![]() .
.
分①若 3是某列的和,②若3是某行的和,討論均可得出矛盾,綜上,不存在“5階![]() 表”.
表”.
試題解析:
(I)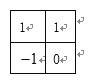 ;
;
(II)對任意一個(gè)“![]() 階
階![]() 表”,
表”, ![]() 表示第
表示第![]() 行所有數(shù)的和,
行所有數(shù)的和, ![]() 表示第
表示第![]() 列所有數(shù)的和
列所有數(shù)的和
(![]() ).
). ![]() 與
與![]() 均表示數(shù)表中所有數(shù)的和,所以
均表示數(shù)表中所有數(shù)的和,所以![]()
![]() .
.
因?yàn)?/span>![]() ,所以
,所以![]() 只能取
只能取![]() 內(nèi)的整數(shù).
內(nèi)的整數(shù).
又因?yàn)?/span>![]() 互不相等,
互不相等, ![]() 且
且![]() ,
,
所以![]() ,
,
所以![]()
![]()
![]()
![]() .
.
所以![]()
![]() 為偶數(shù).
為偶數(shù).
(III)假設(shè)存在一個(gè)“![]() 階
階![]() 表”,則由(II)知
表”,則由(II)知![]() ,且
,且![]() 和
和![]() 至少有一個(gè)成立,不妨設(shè)
至少有一個(gè)成立,不妨設(shè)![]() .
.
設(shè)![]() ,則
,則![]() ,于是
,于是![]() ,因而可設(shè)
,因而可設(shè)![]() ,
,
![]() ,
, ![]() .
.
①若 3是某列的和,由于![]() ,故只能是前四列某列的和,不妨設(shè)是第一列,即
,故只能是前四列某列的和,不妨設(shè)是第一列,即![]() .現(xiàn)考慮
.現(xiàn)考慮![]() ,只能是
,只能是![]() 或
或![]() ,不妨設(shè)
,不妨設(shè)![]() ,即
,即![]() ,由
,由![]() 兩兩不等知
兩兩不等知![]() 兩兩不等,不妨設(shè)
兩兩不等,不妨設(shè)![]() ,若
,若![]() 則
則![]() ;若
;若![]() 則
則![]() ;若
;若![]() 則
則![]() ,均與已知矛盾.
,均與已知矛盾.
②若3是某行的和,不妨設(shè)![]() ,則第4行至少有3個(gè)1,若這3個(gè)1是前四個(gè)中某三個(gè)數(shù),不妨設(shè)
,則第4行至少有3個(gè)1,若這3個(gè)1是前四個(gè)中某三個(gè)數(shù),不妨設(shè)![]() ,則第五行前三個(gè)數(shù)只能是3個(gè)不同的數(shù),不妨設(shè)
,則第五行前三個(gè)數(shù)只能是3個(gè)不同的數(shù),不妨設(shè)
![]() ,則
,則![]() 矛盾,故第四行只能前四個(gè)數(shù)有2個(gè)1,第五個(gè)數(shù)為1,不妨設(shè)
矛盾,故第四行只能前四個(gè)數(shù)有2個(gè)1,第五個(gè)數(shù)為1,不妨設(shè)![]() ,所以
,所以![]() ,第五行只能是2個(gè)0,3個(gè)
,第五行只能是2個(gè)0,3個(gè)![]() 或1個(gè)1,4個(gè)
或1個(gè)1,4個(gè)![]() .則
.則![]() 至少有兩個(gè)數(shù)相同,不妨設(shè)
至少有兩個(gè)數(shù)相同,不妨設(shè)![]() ,則
,則![]() 與已知矛盾.
與已知矛盾.
綜上,不存在“5階![]() 表”.
表”.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 和橢圓
和橢圓![]() ,
, ![]() 是橢圓
是橢圓![]() 的左焦點(diǎn).
的左焦點(diǎn).
(Ⅰ)求橢圓![]() 的離心率和點(diǎn)
的離心率和點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(Ⅱ)點(diǎn)![]() 在橢圓
在橢圓![]() 上,過
上,過![]() 作
作![]() 軸的垂線,交圓
軸的垂線,交圓![]() 于點(diǎn)
于點(diǎn)![]() (
(![]() 不重合),
不重合),![]() 是過點(diǎn)
是過點(diǎn)![]() 的圓
的圓![]() 的切線.圓
的切線.圓![]() 的圓心為點(diǎn)
的圓心為點(diǎn)![]() ,半徑長為
,半徑長為![]() .試判斷直線
.試判斷直線![]() 與圓
與圓![]() 的位置關(guān)系,并證明你的結(jié)論.
的位置關(guān)系,并證明你的結(jié)論.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法的錯誤的是( )
A. 經(jīng)過定點(diǎn)![]() 的傾斜角不為
的傾斜角不為![]() 的直線的方程都可以表示為
的直線的方程都可以表示為![]()
B. 經(jīng)過定點(diǎn)![]() 的傾斜角不為
的傾斜角不為![]() 的直線的方程都可以表示為
的直線的方程都可以表示為![]()
C. 不經(jīng)過原點(diǎn)的直線的方程都可以表示為![]()
D. 經(jīng)過任意兩個(gè)不同的點(diǎn)![]() 、
、![]() 直線的方程都可以表示為
直線的方程都可以表示為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有下列說法
①互斥事件不一定是對立事件,對立事件一定是互斥事件
②演繹推理是從特殊到一般的推理,它的一般模式是“三段論”
③殘差圖的帶狀區(qū)域的寬度越窄,說明模型擬合精度越高,回歸方程的預(yù)報(bào)精度越高
④若![]() ,則事件
,則事件![]() 與
與![]() 互斥且對立
互斥且對立
⑤甲乙兩艘輪船都要在某個(gè)泊位停靠4小時(shí),假定它們在一晝夜的時(shí)間段中隨機(jī)到達(dá),則這兩艘船中至少有一艘在停靠泊位時(shí)必須等待的概率為![]() .
.
其中正確的說法是______(寫出全部正確說法的序號).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象所過的定點(diǎn)為
的圖象所過的定點(diǎn)為![]() ,光線沿直線
,光線沿直線![]() 射入,遇直線
射入,遇直線![]() 后反射,且反射光線所在的直線
后反射,且反射光線所在的直線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,求
,求![]() 的值和
的值和![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某小區(qū)為美化環(huán)境,建設(shè)美麗家園,計(jì)劃在一塊半徑為R(R為常數(shù))的扇形區(qū)域上,建個(gè)矩形的花壇CDEF和一個(gè)三角形的水池FCG.其中![]() ,O為圓心,
,O為圓心,![]() ,C,G,F在扇形圓弧上,D,E分別在半徑OA,OB上,記OG與CF,DE分別交于M,N,
,C,G,F在扇形圓弧上,D,E分別在半徑OA,OB上,記OG與CF,DE分別交于M,N,![]() .
.
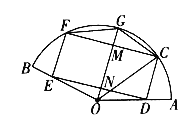
(1)求△FCG的面積S關(guān)于![]() 的關(guān)系式,并寫出定義域;
的關(guān)系式,并寫出定義域;
(2)若R=10米,花壇每平方米的造價(jià)是300元,試問矩形花壇的最高造價(jià)是多少?(取![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】大連市某企業(yè)為確定下一年投入某種產(chǎn)品的宣傳費(fèi),需了解年宣傳費(fèi)![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位:![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費(fèi)
(單位:千元)的影響,對近8年的年宣傳費(fèi)![]() 和年銷售量
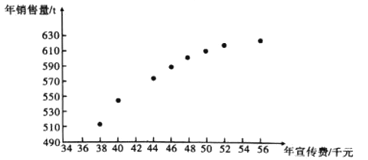
和年銷售量![]() 數(shù)據(jù)作了初步處理,得到下面的散點(diǎn)圖及一些統(tǒng)計(jì)量的值.
數(shù)據(jù)作了初步處理,得到下面的散點(diǎn)圖及一些統(tǒng)計(jì)量的值.
|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
![]() 根據(jù)散點(diǎn)圖判斷,
根據(jù)散點(diǎn)圖判斷,![]() 與
與![]() 哪一個(gè)適宜作為年銷售量
哪一個(gè)適宜作為年銷售量![]() 關(guān)于年宣傳費(fèi)
關(guān)于年宣傳費(fèi)![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
![]() 根據(jù)
根據(jù)![]() 的判斷結(jié)果及表中數(shù)據(jù),建立
的判斷結(jié)果及表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
![]() 已知這種產(chǎn)品的年利潤
已知這種產(chǎn)品的年利潤![]() 與
與![]() 、
、![]() 的關(guān)系為
的關(guān)系為![]() .根據(jù)
.根據(jù)![]() 的結(jié)果回答下列問題:
的結(jié)果回答下列問題:
![]() 年宣傳費(fèi)
年宣傳費(fèi)![]() 時(shí),年銷售量及年利潤的預(yù)報(bào)值是多少?
時(shí),年銷售量及年利潤的預(yù)報(bào)值是多少?
![]() 年宣傳費(fèi)
年宣傳費(fèi)![]() 為何值時(shí),年利潤的預(yù)報(bào)值最大?
為何值時(shí),年利潤的預(yù)報(bào)值最大?
附:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計(jì)分別為:
的斜率和截距的最小二乘估計(jì)分別為:
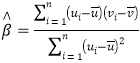 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() =1(a>b>0)的右焦點(diǎn)為F(2,0),且過點(diǎn)(2
=1(a>b>0)的右焦點(diǎn)為F(2,0),且過點(diǎn)(2![]() ,
,![]() ).
).
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)設(shè)直線l:y=kx(k>0)與橢圓在第一象限的交點(diǎn)為M,過點(diǎn)F且斜率為-1的直線與l交于點(diǎn)N,若![]() sin∠FON(O為坐標(biāo)原點(diǎn)),求k的值.
sin∠FON(O為坐標(biāo)原點(diǎn)),求k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的最大值為
的最大值為![]() ,其圖像相鄰兩條對稱軸之間的距離為
,其圖像相鄰兩條對稱軸之間的距離為![]() ,且
,且![]() 的圖像關(guān)于點(diǎn)
的圖像關(guān)于點(diǎn)![]() 對稱,則下列判斷正確的是()
對稱,則下列判斷正確的是()
A. 函數(shù)![]() 在
在![]() 上單調(diào)遞增
上單調(diào)遞增
B. 函數(shù)![]() 的圖像關(guān)于直線
的圖像關(guān)于直線![]() 對稱
對稱
C. 當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的最小值為
的最小值為![]()
D. 要得到函數(shù)![]() 的圖像,只需要
的圖像,只需要![]() 將的圖像向右平移
將的圖像向右平移![]() 個(gè)單位
個(gè)單位
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com