
【題目】小王投資1萬元2萬元、3萬元獲得的收益分別是4萬元、9萬元、16萬元為了預測投資資金x(萬元)與收益y萬元)之間的關系,小王選擇了甲模型![]() 和乙模型
和乙模型![]() .
.
(1)根據小王選擇的甲、乙兩個模型,求實數a,b,c,p,q,r的值
(2)若小王投資4萬元,獲得收益是25.2萬元,請問選擇哪個模型較好?
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,如果![]() 與
與![]() 都是整數,就稱點
都是整數,就稱點![]() 為整點,下列命題中正確的是_____________(寫出所有正確命題的編號)
為整點,下列命題中正確的是_____________(寫出所有正確命題的編號)
①存在這樣的直線,既不與坐標軸平行又不經過任何整點
②如果![]() 與
與![]() 都是無理數,則直線
都是無理數,則直線![]() 不經過任何整點
不經過任何整點
③直線![]() 經過無窮多個整點,當且僅當
經過無窮多個整點,當且僅當![]() 經過兩個不同的整點
經過兩個不同的整點
④直線![]() 經過無窮多個整點的充分必要條件是:
經過無窮多個整點的充分必要條件是:![]() 與
與![]() 都是有理數
都是有理數
⑤存在恰經過一個整點的直線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() ,
,![]() 為兩條異面直線,
為兩條異面直線,![]() ,
,![]() 為兩個平面,
為兩個平面,![]() ,
,![]() ,
,![]() ,則下列結論中錯誤的序號是______.
,則下列結論中錯誤的序號是______.
①![]() 至少與
至少與![]() ,
,![]() 中一條相交; ②
中一條相交; ②![]() 至多與
至多與![]() ,
,![]() 中一條相交;
中一條相交;
③![]() 至少與
至少與![]() ,
,![]() 中一條平行; ④
中一條平行; ④![]() 必與
必與![]() ,
,![]() 中一條相交,與另一條平行.
中一條相交,與另一條平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是( )
A.“![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
B.對于命題![]() :
:![]() ,使得
,使得![]() ,則
,則![]() :
:![]() 均有
均有![]()
C.若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為假命題
均為假命題
D.命題“若![]() ,則
,則![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() ”
”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐S—ABCD中,∠SDA=2∠SAD=90°,∠BAD+∠ADC=180°,AB=![]() CD,點F是線段
CD,點F是線段
SA上靠近點A的一個三等分點,AC與BD相交于E.

(1)在線段SB上作出點G,使得平面EFG∥平面SCD,請指明點G的具體位置,并用陰影部分表示平面EFG,不必說明平面EFG∥平面SCD的理由;
(2)若SA=SB=2,AB=AD=BD=![]() ,求點F到平面SCD的距離.
,求點F到平面SCD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲乙兩組學生,分別參加某項體能測試,所得成績的莖葉圖如圖.規定測試成績大于等于90分為優秀,80至89分為良好,60至79分為合格,60分以下為不合格.
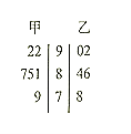
(1)現從甲組數據中抽取一名學生的成績,有放回地抽取6次,記抽到優秀成績的次數為X,求![]() ;
;
(2)從甲、乙兩組學生中任取3名學生,記抽中成績優秀的學生數為Y,求Y的概率分布與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]()
![]()
![]() ,若
,若![]() ,且
,且![]() 的圖象相鄰的對稱軸間的距離不小于
的圖象相鄰的對稱軸間的距離不小于![]() .
.
(1)求![]() 的取值范圍.
的取值范圍.
(2)若當![]() 取最大值時,
取最大值時, ![]() ,且在
,且在![]() 中,
中, ![]() 分別是角
分別是角![]() 的對邊,其面積
的對邊,其面積![]() ,求
,求![]() 周長的最小值.
周長的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com