【題目】已知函數(shù)
，曲線
在點(diǎn)
處的切線平行于
軸.
（1）求
的單調(diào)區(qū)間；
（2）證明：當(dāng)
時(shí)，
恒成立.
【答案】（1）遞減區(qū)間為
，遞增區(qū)間為
；（2）證明見解析．
【解析】
試題分析：（1）本題首先由導(dǎo)數(shù)的幾何意義知
，從而求得
值，然后通過
確定增區(qū)間，
確定減區(qū)間；（2）考慮到
，因此首先證明特殊情況，
的情況，此時(shí)研究函數(shù)
，求出導(dǎo)函數(shù)
，為了確定
的正負(fù)，設(shè)
并求導(dǎo)得
，考慮到式子中的
，可分類證明
和
時(shí)都有
，即
單調(diào)遞增，因此
即
只有唯一解
，正負(fù)隨之而定，從而得
，于是結(jié)論得證．再由不等式的性質(zhì)
也得證．
試題解析：（1）由
，依題意，
，有
，所以
，顯然
在
上單調(diào)遞增，且，故當(dāng)
，當(dāng)
，所以函數(shù)
的遞減區(qū)間為，遞增區(qū)間為.
（2）設(shè)
.
①當(dāng)
時(shí)，，設(shè)
則.
當(dāng)
時(shí)，
，當(dāng)
時(shí)，
，則
，所以
單增且
故當(dāng)
，當(dāng) 
，所以
.
②
時(shí)，因?yàn)?/span>
所以
有①知
綜上所述，當(dāng)
時(shí)，
恒成立.
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)y＝f(x)的導(dǎo)函數(shù)y＝f′(x)的圖象如圖所示，給出下列命題：
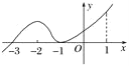
①－3是函數(shù)y＝f(x)的極值點(diǎn)；
②－1是函數(shù)y＝f(x)的最小值點(diǎn)；
③y＝f(x)在區(qū)間(－3,1)上單調(diào)遞增；
④y＝f(x)在x＝0處切線的斜率小于零．
以上正確命題的序號(hào)是( )
A. ①②B. ③④C. ①③D. ②④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
和
（
且為常數(shù)），則下列結(jié)論正確的是（ ）
A.當(dāng)
時(shí)，存在實(shí)數(shù)
，使得關(guān)于
的方程
有四個(gè)不同的實(shí)數(shù)根
B.存在
，使得關(guān)于的方程有三個(gè)不同的實(shí)數(shù)根
C.當(dāng)
時(shí)，若函數(shù)
恰有
個(gè)不同的零點(diǎn)
、
、
，則
D.當(dāng)
時(shí)，且關(guān)于的方程有四個(gè)不同的實(shí)數(shù)根、、、
，若
在
上的最大值為
，則
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列
的前
項(xiàng)和為
，且
，
（
）.
（1）計(jì)算
，
，
，
，并求數(shù)列的通項(xiàng)公式；
（2）若數(shù)列
滿足
，求證：數(shù)列是等比數(shù)列；
（3）由數(shù)列的項(xiàng)組成一個(gè)新數(shù)列
：
，
，
，
，
，設(shè)
為數(shù)列的前項(xiàng)和，試求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，其中
為實(shí)常數(shù)．
（Ⅰ）判斷
的奇偶性；
（Ⅱ）若對(duì)任意
，使不等式
恒成立，求的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知奇函數(shù)
的定義域?yàn)閇-1,1]，當(dāng)
時(shí)，
。
（1）求函數(shù)在
上的值域；
（2）若
時(shí)，函數(shù)
的最小值為-2，求實(shí)數(shù)λ的值。
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】甲乙二人用4張撲克牌（分別是紅桃2，紅桃3，紅桃4，方片4）完游戲，他們將撲克牌洗勻后，背面朝上放在桌面上，甲先抽，乙后抽，抽出的牌不放回，各抽一張.
（1）設(shè)
分別表示甲、乙抽到的牌的數(shù)字，寫出甲乙二人抽到的牌的所有情況；
（2）若甲抽到紅桃3，則乙抽出的牌的牌面數(shù)字比3大的概率是多少？
（3）甲乙約定：若甲抽到的牌的牌面數(shù)字比乙大，則甲勝，反之，則乙勝，你認(rèn)為此游戲是否公平，說明你的理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】甲乙兩人玩一種游戲，每次由甲、乙各出1到5根手指，若和為偶數(shù)算甲贏，否則算乙贏.
（1）若以
表示和為6的事件，求
；
（2）現(xiàn)連玩三次，若以
表示甲至少贏一次的事件，
表示乙至少贏兩次的事件，試問
與
是否為互斥事件？為什么？
（3）這種游戲規(guī)則公平嗎？試說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某險(xiǎn)種的基本保費(fèi)為
（單位：元），繼續(xù)購買該險(xiǎn)種的投保人稱為續(xù)保人，續(xù)保人本年度的保費(fèi)與其
上年度出險(xiǎn)次數(shù)的關(guān)聯(lián)如下：
上年度出險(xiǎn)次數(shù) | 0 | 1 | 2 | 3 | 4 |
|
保費(fèi) |
|
|
|
|
|
|
隨機(jī)調(diào)查了該險(xiǎn)種的200名續(xù)保人在一年內(nèi)的出險(xiǎn)情況，得到如下統(tǒng)計(jì)表：
出險(xiǎn)次數(shù) | 0 | 1 | 2 | 3 | 4 |
|
頻數(shù) | 60 | 50 | 30 | 30 | 20 | 10 |
（1）記A為事件：“一續(xù)保人本年度的保費(fèi)不高于基本保費(fèi)”.求
的估計(jì)值；
（2）記B為事件：“一續(xù)保人本年度的保費(fèi)高于基本保費(fèi)但不高于基本保費(fèi)的160％”.求
的估計(jì)值；
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
