【題目】考察下列無窮數(shù)列，判斷是否有極限，若有，求出極限；若沒有，請說明理由．
（1）
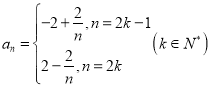
（2）
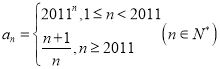
（3）
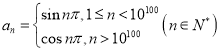
【答案】（1）極限不存在，理由見解析；（2）極限為
；（3）極限不存在．理由見解析.
【解析】
（1）根據(jù)
和
時，
趨近的常數(shù)不同可知極限不存在；
（2）當(dāng)
時，可知無限趨近于，由此求得極限；
（3）當(dāng)
時，始終等于或
兩個值，可知極限不存在.
（1）當(dāng)且
無限增大時，
無限趨近于
，則無限趨近于
；
當(dāng)且無限增大時，無限趨近于，則無限趨近于
；
當(dāng)
無限增大時，不趨近于一個確定的常數(shù)，該數(shù)列的極限不存在．
（2）當(dāng)
時，的值小于
；
當(dāng)時，
，即無限趨近于，
當(dāng)無限增大時，趨近于一個確定的常數(shù)，該數(shù)列的極限為．
（3）當(dāng)時，
，
當(dāng)n無限增大時，始終等于或兩個值，該數(shù)列的極限不存在．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某高中志愿者部有男志愿者6人，女志愿者4人，這些人要參加元旦聯(lián)歡會的服務(wù)工作. 從這些人中隨機抽取4人負責(zé)舞臺服務(wù)工作，另外6人負責(zé)會場服務(wù)工作.
（Ⅰ）設(shè)
為事件：“負責(zé)會場服務(wù)工作的志愿者中包含女志愿者
但不包含男志愿者
”，求事件發(fā)生的概率.
（Ⅱ）設(shè)
表示參加舞臺服務(wù)工作的女志愿者人數(shù)，求隨機變量的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】對于給定數(shù)列
，如果存在實常數(shù)
使得
對于任意
都成立，我們稱數(shù)列是“M類數(shù)列”．
（1）若
，數(shù)列
是否為“M類數(shù)列”？若是，指出它對應(yīng)的實常數(shù)；若不是，請說明理由；
（2）證明：若數(shù)列
是“M類數(shù)列”，則數(shù)列
也是“M類數(shù)列”．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在數(shù)列
中，若
是正整數(shù)，且
，…，則稱為“絕對差數(shù)列”.
（1）舉出一個前5項不為零的“絕對差數(shù)列”（只要求寫出前10項）；
（2）若“絕對差數(shù)列”中，
，數(shù)列
滿足
，
，…，分別判斷當(dāng)
時，
與
的極限是否存在？如果存在，求出其極限值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某電器商場銷售的彩電、U盤和
播放器三種產(chǎn)品.該商場的供貨渠道主要是甲、乙兩個品牌的二級代理商.今年9月份，該商場從每個代理商處各購得彩電100臺、U盤52個、播放器180臺.而10月份，該商場從每個代理商處購得的產(chǎn)品數(shù)量都是9月份的1.5倍.現(xiàn)知甲、乙兩個代理商給出的產(chǎn)品單價（元）如下頁表中所示：
彩電 | U盤 |
| |
甲代理商單價（元） | 2350 | 1200 | 750 |
乙代理商單價（元） | 2100 | 920 | 700 |
（1）計算
，并指出結(jié)果的實際意義；
（2）用矩陣求該商場在這兩個月中分別支付給兩個代理商的購貨費用.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知在等比數(shù)列{an}中，
＝2，，
＝128，數(shù)列{bn}滿足b1＝1，b2＝2，且{
}為等差數(shù)列．
（1）求數(shù)列{an}和{bn}的通項公式；
（2）求數(shù)列{bn}的前n項和．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系xOy中，直線l的參數(shù)方程為
（t為參數(shù)），以坐標(biāo)原點為極點，x軸的非負半軸為極軸且取相同的單位長度建立極坐標(biāo)系，已知曲線C的極坐標(biāo)方程為
，且直線l經(jīng)過曲線C的左焦點F．
（1）求直線l的普通方程；
（2）設(shè)曲線C的內(nèi)接矩形的周長為L，求L的最大值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】銷售某種活海鮮，根據(jù)以往的銷售情況，按日需量
（公斤）屬于[0，100)，[100，200)，[200，300)，[300，400)，[400，500]進行分組，得到如圖所示的頻率分布直方圖．這種海鮮經(jīng)銷商進價成本為每公斤20元，當(dāng)天進貨當(dāng)天以每公斤30元進行銷售，當(dāng)天未售出的須全部以每公斤10元賣給冷凍庫．某海鮮產(chǎn)品經(jīng)銷商某天購進了300公斤這種海鮮，設(shè)當(dāng)天利潤為
元．
（I）求關(guān)于的函數(shù)關(guān)系式；
（II）結(jié)合直方圖估計利潤
不小于800元的概率．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，直線
與拋物線
相交于
兩點，與
軸交于點
，且
，
于點
.
（1）當(dāng)
時，求
的值；
（2）當(dāng)
時，求
與
的面積之積
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com