
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(Ⅱ)當![]() 時,證明
時,證明![]() .
.
【答案】(Ⅰ)詳見解析;(Ⅱ)詳見解析.
【解析】試題分析:(Ⅰ)易求得函數![]() 的定義域為
的定義域為![]() ,由函數
,由函數![]() ,則
,則![]() ,令
,令![]() 或
或![]() ,即可求得函數
,即可求得函數![]() 的單調區間;
的單調區間;
(Ⅱ)當![]() 時,
時, ![]() ,要證
,要證![]() ,只需證
,只需證![]() ,所以此問就是求函數
,所以此問就是求函數![]() 在定義域區間的最小值.
在定義域區間的最小值.
試題解析: (Ⅰ)易求得函數![]() 的定義域為
的定義域為![]() ,
,
已知函數![]() ,
,
所以![]() ,
,
令![]() ,即
,即![]()
當![]() 時,
時, ![]() 恒成立,所以函數
恒成立,所以函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,無單調遞減區間。
,無單調遞減區間。
當![]() 時,不等式
時,不等式![]() 的解為
的解為![]() 或
或![]()
又因為![]() ,
,
所以函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間為
,單調遞減區間為![]()
當![]() 時,不等式
時,不等式![]() 的解為
的解為![]() 或
或![]()
又因為![]() ,
, ![]()
所以函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間為
,單調遞減區間為![]()
綜上所述,當![]() 時,函數
時,函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,無單調遞減區間。
,無單調遞減區間。
當![]() 時,函數
時,函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間為
,單調遞減區間為![]()
當![]() 時,函數
時,函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間為
,單調遞減區間為![]()
(Ⅱ)當![]() 時,
時, ![]()
所以![]()
已知![]()
令![]() ,得
,得![]()
所以函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間為
,單調遞減區間為![]()
所以![]()
所以![]()


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
【題目】根據教育部最新消息,2020年高考數學將是最后一年實行文理分科,由于課程大綱與命題方向出現了變動,試題難度也可能會做出相應調整.為了評估學生在2020年高考復習情況,某中學組織本校540名考生參加市模擬考試,現采用分層抽樣的方法從文、理科考生中分別抽取60和30份數學試卷進行成績分析,得到下面的成績頻數分布表:
分數分組 |
|
|
|
|
|
文科頻數 | 12 | 4 | 10 | 11 | 23 |
理科頻數 | 3 | 7 | 2 | 10 | 8 |
由此可估計文科考生的不及格人數(90分為及格分數線)大約為( )
A.128B.156C.204D.132
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】表示一位騎自行車和一位騎摩托車的旅行者在相距80 km的甲、乙兩城間從甲城到乙城所行駛的路程與時間之間的函數關系,有人根據函數圖象,提出了關于這兩個旅行者的如下信息:

①騎自行車者比騎摩托車者早出發3 h,晚到1 h;
②騎自行車者是變速運動,騎摩托車者是勻速運動;
③騎摩托車者在出發1.5 h后追上了騎自行車者;
④騎摩托車者在出發1.5 h后與騎自行車者速度一樣.
其中,正確信息的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某銀行對某市最近5年住房貸款發放情況(按每年6月份與前一年6月份為1年統計)作了統計調查,得到如下數據:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
貸款 | 50 | 60 | 70 | 80 | 100 |
(1)將上表進行如下處理:![]() ,
,
得到數據:
| 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
試求![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ,再寫出
,再寫出![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)利用(1)中所求的線性回歸方程估算2019年房貸發放數額.
參考公式: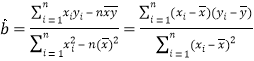 ,
, ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com