Question

（08年赤峰二中模擬理）  已知正三棱柱ABC - A₁B₁C₁中, AA₁ = 2AC = 4, 延長CB至D, 使CB = BD.

   （I）求證: 直線C₁B // 平面AB₁D;

   （II）求平面AB₁D與平面ACB所成角.

 

Answer 1

解析：法一: (Ⅰ) 因為 C₁B₁ = CB = DB, 且C₁B₁ // BD,

∴ 四邊形C₁BDB₁是平行四邊形,

∴ C₁B // B₁D，

又B₁D Ì 平面AB₁D,

∴ 直線C₁B // 平面AB₁D.

(Ⅱ) 過B₁作B₁H ^ AD于H, 連結(jié)BH.

∵ B₁B ^ 平面ACD,

∴ BH ^ AD

∴ Ð B₁HB是平面AB₁D平面ACB所成角的平面角.

在△ACD中, 由于CB = BD = BA,

∴ ∠DAC = 90°,

∴ BH =AC,

∵ AA₁ = 2AC = 4,

∴ tanÐB₁HB == 4,

∴ 平面AB₁D平面ACB所成角為arctan4.

 

法二: 在△ACD中, 由于CB = BD = BA,

∴ ∠DAC=90°,

如圖, 以A為原點, 以AD為x軸正向, 建立空間直角坐標系O - xyz,

∵ 正三棱柱ABC - A₁B₁C₁中, AA₁ = 2AC = 4,

∴ A(0, 0, 0), B(, 1, 0), B₁(, 1, 4),

C₁(0, 2, 4), D(2, 0, 0).

(Ⅰ) ∵= (-, 1, 4),= (-, 1, 4),

∴//

又BC₁ Ë 平面AB₁D, B1D Ì 平面AB₁D,

∴ 直線C₁B // 平面AB₁D.

(Ⅱ) =(2, 0, 0), = (, 1, 4), 設(shè)平面AB₁D的法向量n = (x, y, z), 則

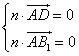, 即 , ∴ ,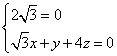

取z = 1, 則n = (0, - 4, 1), 取平面ACB的法向量為m = (0, 0, 1),

則cos<n, m> =,

∴ 平面AB₁D與平面ACB所成角為arccos.