
【題目】求平面直角坐標系中格點凸五邊形(即每個頂點的縱、橫坐標都是整數的凸五邊形)的周長的最小值。
科目:高中數學 來源: 題型:
【題目】已知數列{an}各項均不相同,a1=1,定義![]() ,其中n,k∈N*.
,其中n,k∈N*.
(1)若![]() ,求
,求![]() ;
;
(2)若bn+1(k)=2bn(k)對![]() 均成立,數列{an}的前n項和為Sn.
均成立,數列{an}的前n項和為Sn.
(i)求數列{an}的通項公式;
(ii)若k,t∈N*,且S1,Sk-S1,St-Sk成等比數列,求k和t的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中點,F是DC上的點且DF=![]() AB,PH為△PAD邊上的高.
AB,PH為△PAD邊上的高.
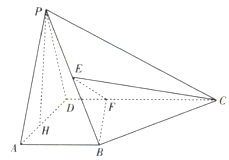
(1)證明:PH⊥平面ABCD;
(2)若PH=1,AD=![]() ,FC=1,求三棱錐E-BCF的體積;
,FC=1,求三棱錐E-BCF的體積;
(3)證明:EF⊥平面PAB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為a,
的棱長為a,![]() 分別是棱
分別是棱![]() 、
、![]() 的中點,過點
的中點,過點![]() 的平面分別與棱
的平面分別與棱![]() 、
、![]() 交于點
交于點![]() ,設
,設![]() ,
,![]() ,給出以下四個命題:
,給出以下四個命題:
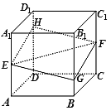
(1)平面![]() 與平面
與平面![]() 所成角的最大值為
所成角的最大值為![]() ;
;
(2)四邊形![]() 的面積的最小值為
的面積的最小值為![]() ;
;
(3)四棱錐![]() 的體積為
的體積為![]() ;
;
(4)點![]() 到平面
到平面![]() 的距離的最大值為
的距離的最大值為![]() ,
,
其中正確的個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘數學家阿波羅尼奧斯(約公元前262~公元前190年)的著作《圓錐曲線論》是古代世界光輝的科學成果,他證明過這樣一個命題:平面內與兩定點距離的比為常數k(k>0,k≠1)的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.在平面直角坐標系中,設A(﹣3,0),B(3,0),動點M滿足![]() =2,則動點M的軌跡方程為()
=2,則動點M的軌跡方程為()
A. (x﹣5)2+y2=16B. x2+(y﹣5)2=9
C. (x+5)2+y2=16D. x2+(y+5)2=9
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com