
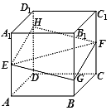
【題目】如圖,正方體![]() 的棱長為a,
的棱長為a,![]() 分別是棱
分別是棱![]() 、
、![]() 的中點,過點
的中點,過點![]() 的平面分別與棱
的平面分別與棱![]() 、
、![]() 交于點
交于點![]() ,設(shè)
,設(shè)![]() ,
,![]() ,給出以下四個命題:
,給出以下四個命題:
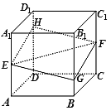
(1)平面![]() 與平面
與平面![]() 所成角的最大值為
所成角的最大值為![]() ;
;
(2)四邊形![]() 的面積的最小值為
的面積的最小值為![]() ;
;
(3)四棱錐![]() 的體積為
的體積為![]() ;
;
(4)點![]() 到平面
到平面![]() 的距離的最大值為
的距離的最大值為![]() ,
,
其中正確的個數(shù)為( )
A.1B.2C.3D.4
【答案】C
【解析】
由兩平面所成角的余弦公式即面積射影公式,計算可得所求最大值,可判斷(1);
由四邊形![]() 為菱形,計算面積,考慮
為菱形,計算面積,考慮![]() 的最小值,可判斷(2);
的最小值,可判斷(2);
由棱錐的等體積法,計算可判斷(3);
由等體積法和函數(shù)的性質(zhì)可判斷(4);
對于(1),由面面平行的性質(zhì)定理可得![]() ,可得四邊形
,可得四邊形![]() 為平行四邊形,又直角梯形
為平行四邊形,又直角梯形![]() 和直角梯形
和直角梯形![]() 全等,可得
全等,可得![]() ,即有四邊形
,即有四邊形![]() 為菱形,且
為菱形,且![]() ,由平面
,由平面![]() 在底面上的射影為四邊形
在底面上的射影為四邊形![]() ,
,
由面積射影公式可得
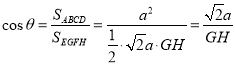
由![]() ,可得
,可得![]() ,可得平面
,可得平面![]() 與平面
與平面![]() 所成角的最大值不為
所成角的最大值不為![]() ,故(1)錯;
,故(1)錯;
對于(2),由![]() ,可得菱形
,可得菱形![]() 的面積的最小值為
的面積的最小值為![]()
故(2)正確;
對于(3),因為四棱錐![]() 的體積為
的體積為
![]() ,故(3)正確;
,故(3)正確;
對于(4)![]()
![]()
設(shè)![]() 到平面
到平面![]() 的距離為
的距離為![]() ,可得
,可得
![]() ,
,
可得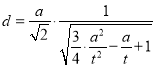 ,(其中
,(其中![]() ),當(dāng)
),當(dāng)![]() 即
即![]() 時,
時,
![]() 取得最大值
取得最大值![]() ,故(4)正確;
,故(4)正確;
故選:C


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知實數(shù)x,y滿足 設(shè)
設(shè)![]() ,則z的取值范圍是______.(
,則z的取值范圍是______.(![]() 表示a,b兩數(shù)中的較大數(shù))
表示a,b兩數(shù)中的較大數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題中正確的是( )
A. 命題![]() :
:![]() ,
,![]() ,則命題
,則命題![]() :
:![]() ,
,![]()
B. “![]() ”是“
”是“![]() ”的充要條件
”的充要條件
C. 命題“若![]() ,則
,則![]() 或
或![]() ”的逆否命題是“若
”的逆否命題是“若![]() 或
或![]() ,則
,則![]() ”
”
D. 命題![]() :
:![]() ,
,![]() ;命題
;命題![]() :對
:對![]() ,總有
,總有![]() ;則
;則![]() 是真命題
是真命題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】求平面直角坐標(biāo)系中格點凸五邊形(即每個頂點的縱、橫坐標(biāo)都是整數(shù)的凸五邊形)的周長的最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在區(qū)間![]() 上的函數(shù)
上的函數(shù)![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱,當(dāng)
對稱,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的表達式;
的表達式;
(3)若關(guān)于![]() 的方程
的方程![]() 有解,那么將方程在
有解,那么將方程在![]() 取某一確定值時所求得的所有解的和記為
取某一確定值時所求得的所有解的和記為![]() ,求
,求![]() 的所有可能值及相應(yīng)
的所有可能值及相應(yīng)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,港口![]() 在港口
在港口![]() 的正東120海里處,小島
的正東120海里處,小島![]() 在港口
在港口![]() 的北偏東
的北偏東![]() 的方向,且在港口
的方向,且在港口![]() 北偏西
北偏西![]() 的方向上,一艘科學(xué)考察船從港口
的方向上,一艘科學(xué)考察船從港口![]() 出發(fā),沿北偏東
出發(fā),沿北偏東![]() 的
的![]() 方向以20海里/小時的速度駛離港口
方向以20海里/小時的速度駛離港口![]() .一艘給養(yǎng)快艇從港口
.一艘給養(yǎng)快艇從港口![]() 以60海里/小時的速度駛向小島
以60海里/小時的速度駛向小島![]() ,在
,在![]() 島轉(zhuǎn)運補給物資后以相同的航速送往科考船.已知兩船同時出發(fā),補給裝船時間為1小時.
島轉(zhuǎn)運補給物資后以相同的航速送往科考船.已知兩船同時出發(fā),補給裝船時間為1小時.
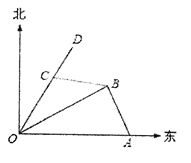
(1)求給養(yǎng)快艇從港口![]() 到小島
到小島![]() 的航行時間;
的航行時間;
(2)給養(yǎng)快艇駛離港口![]() 后,最少經(jīng)過多少小時能和科考船相遇?
后,最少經(jīng)過多少小時能和科考船相遇?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義域為![]() 的單調(diào)函數(shù)
的單調(diào)函數(shù)![]() 滿足
滿足![]()
![]() ,且
,且![]() ,
,
(1)求![]() ,
,![]() ;
;
(2)判斷函數(shù)![]() 的奇偶性,并證明;
的奇偶性,并證明;
(3)若對于任意![]() 都有
都有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com