
【題目】已知點![]() ,
,![]() 是圓
是圓![]() 上的一個動點,
上的一個動點,![]() 為圓心,線段
為圓心,線段![]() 的垂直平分線與直線
的垂直平分線與直線![]() 的交點為
的交點為![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設(shè)![]() 與
與![]() 軸的正半軸交于點
軸的正半軸交于點![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() 兩點(
兩點(![]() 不經(jīng)過
不經(jīng)過![]() 點),且
點),且![]() ,證明:直線
,證明:直線![]() 經(jīng)過定點,并寫出該定點的坐標(biāo).
經(jīng)過定點,并寫出該定點的坐標(biāo).
【答案】(1)![]() ;(2)直線
;(2)直線![]() 經(jīng)過定點
經(jīng)過定點![]() .
.
【解析】
(1)由橢圓定義,得到點![]() 的軌跡
的軌跡![]() 是以
是以![]() 、
、![]() 為焦點的橢圓,求得
為焦點的橢圓,求得![]() 的值,進(jìn)而得到
的值,進(jìn)而得到![]() 的值,即可得到橢圓的標(biāo)準(zhǔn)方程;
的值,即可得到橢圓的標(biāo)準(zhǔn)方程;
(2)聯(lián)立方程組,利用二次方程根與系數(shù)的關(guān)系,求得![]() ,
,![]() ,得到
,得到![]() ,
,![]() ,再由
,再由![]() ,根據(jù)
,根據(jù)![]() ,即可求解實數(shù)m的值,進(jìn)而得出結(jié)論.
,即可求解實數(shù)m的值,進(jìn)而得出結(jié)論.
(1)圓![]() 的圓心
的圓心![]() ,半徑
,半徑![]() ,
,
由垂直平分線性質(zhì)知:![]() ,
,
故![]() ,
,
由橢圓定義知,點![]() 的軌跡
的軌跡![]() 是以
是以![]() 、
、![]() 為焦點的橢圓,
為焦點的橢圓,
設(shè)![]() :
:![]() ,焦距為
,焦距為![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() 的方程為
的方程為![]() .
.
(2)由已知得![]() ,由
,由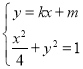 得
得![]() ,
,
當(dāng)![]() 時,設(shè)
時,設(shè)![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由![]() 得
得![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]() ,
,
①當(dāng)![]() 時,直線
時,直線![]() 經(jīng)過點
經(jīng)過點![]() ,不符合題意,舍去.
,不符合題意,舍去.
②當(dāng)![]() 時,顯然有
時,顯然有![]() ,直線
,直線![]() 經(jīng)過定點
經(jīng)過定點![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某廠生產(chǎn)某種產(chǎn)品的年固定成本為250萬元,每生產(chǎn)![]() 千件,需另投入成本
千件,需另投入成本![]() ,當(dāng)年產(chǎn)量不足80千件時,
,當(dāng)年產(chǎn)量不足80千件時,![]() (萬元);當(dāng)年產(chǎn)量不小于80千件時,
(萬元);當(dāng)年產(chǎn)量不小于80千件時,![]() (萬元),每件售價為0.05萬元,通過市場分析,該廠生產(chǎn)的商品能全部售完.
(萬元),每件售價為0.05萬元,通過市場分析,該廠生產(chǎn)的商品能全部售完.
(1)寫出年利潤![]() (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量![]() (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(2)年產(chǎn)量為多少千件時,該廠在這一商品的生產(chǎn)中所獲利潤最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是某學(xué)校研究性課題《什么樣的活動最能促進(jìn)同學(xué)們進(jìn)行垃圾分類》向題的統(tǒng)計圖(每個受訪者都只能在問卷的5個活動中選擇一個),以下結(jié)論錯誤的是( )

A. 回答該問卷的總?cè)藬?shù)不可能是100個
B. 回答該問卷的受訪者中,選擇“設(shè)置分類明確的垃圾桶”的人數(shù)最多
C. 回答該問卷的受訪者中,選擇“學(xué)校團(tuán)委會宣傳”的人數(shù)最少
D. 回答該問卷的受訪者中,選擇“公益廣告”的人數(shù)比選擇“學(xué)校要求”的少8個
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓![]() (
(![]() )的一個焦點
)的一個焦點![]() 點
點![]() 為橢圓
為橢圓![]() 內(nèi)一點,若橢圓
內(nèi)一點,若橢圓![]() 上存在一點
上存在一點![]() ,使得
,使得![]() ,則橢圓
,則橢圓![]() 的離心率的取值范圍是( )
的離心率的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在棱長均相等的正四棱錐![]() 中,
中, ![]() 為底面正方形的重心,
為底面正方形的重心, ![]() 分別為側(cè)棱
分別為側(cè)棱![]() 的中點,有下列結(jié)論:
的中點,有下列結(jié)論:
①![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③
;③![]() ;
;
④直線![]() 與直線
與直線![]() 所成角的大小為
所成角的大小為![]() .
.
其中正確結(jié)論的序號是__________.(寫出所有正確結(jié)論的序號)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】 設(shè)f(x)、g(x)分別是定義在R上的奇函數(shù)和偶函數(shù),當(dāng)x<0時,f′(x)·g(x)+f(x)·g′(x)>0,且f(-3)·g(-3)=0,則不等式f(x)·g(x)<0的解集是( )
A. (-3,0)∪(3,+∞)
B. (-3,0)∪ (0,3)
C. (-∞,-3)∪(3,+∞)
D. (-∞,-3)∪(0,3)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() 于點
于點![]() ,將
,將![]() 沿
沿![]() 折起,使
折起,使![]() ,連接
,連接![]() ,得到如圖所示的幾何體.
,得到如圖所示的幾何體.
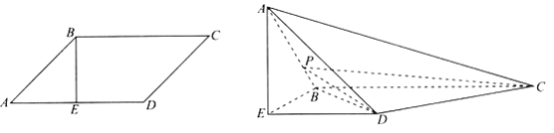
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若點![]() 在線段
在線段![]() 上,直線
上,直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,A,B,C所對的邊分別為a,b,c且ccosA=4,asinC=5.
(1)求邊長c;
(2)著△ABC的面積S=20.求△ABC的周長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com