
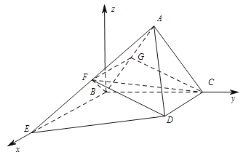
【題目】如圖所示,正三角形ABC所在平面與梯形BCDE所在平面垂直,![]() ,
,![]() =4 ,
=4 ,![]() ,F為棱AE的中點.
,F為棱AE的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析,;(2)![]()
【解析】(1)如圖,取![]() 中點
中點![]() ,連接
,連接![]() 、
、![]() ,因為
,因為![]() 為
為![]() 中點,所以
中點,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() .又
.又![]() 為正三角形,所以
為正三角形,所以
![]() ,從而
,從而![]() , (2分)
, (2分)
由![]() ,
,![]() ,可得
,可得![]() ,由平面ABC
,由平面ABC![]() 平面BCDE,平面ABC
平面BCDE,平面ABC![]() 平面BCDE=BC,
平面BCDE=BC,
可得![]() 平面ABC,因為
平面ABC,因為![]() 平面ABC,所以
平面ABC,所以![]() ,
,
因為![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .(5分)
.(5分)
(2)因為![]() ,
,![]() ,所以
,所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 為
為![]() 與平面
與平面![]() 所成的角,即
所成的角,即![]() ,從而
,從而![]() .(7分)
.(7分)
以![]() 為原點,建立如圖所示的空間直角坐標(biāo)系
為原點,建立如圖所示的空間直角坐標(biāo)系![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,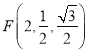 ,
,
所以![]() ,
,![]() .(8分)
.(8分)
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,即
,即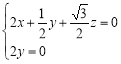 ,解得
,解得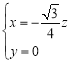 .
.
令![]() ,得
,得![]() .
.
由(1)可知![]() 平面
平面![]() ,所以
,所以![]() 為平面
為平面![]() 的一個法向量.
的一個法向量.
所以![]() .
.
因為二面角![]() 為鈍角,所以其余弦值為
為鈍角,所以其余弦值為![]() .(12分)
.(12分)


 長江作業(yè)本同步練習(xí)冊系列答案
長江作業(yè)本同步練習(xí)冊系列答案 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知橢圓的左焦點為![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() ,
,![]() (
(![]() 都在
都在![]() 軸上方),且
軸上方),且![]() .
.
(ⅰ)若點![]() 的橫坐標(biāo)為1,求
的橫坐標(biāo)為1,求![]() 的面積;
的面積;
(ⅱ)直線![]() 是否恒過定點?若過定點,求出該定點的坐標(biāo);若不過定點,請說明理由.
是否恒過定點?若過定點,求出該定點的坐標(biāo);若不過定點,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4—4:坐標(biāo)系與參數(shù)方程
已知直線l經(jīng)過點![]() ,傾斜角
,傾斜角![]() ,圓
,圓![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)寫出直線l的參數(shù)方程,并把圓![]() 的方程化為直角坐標(biāo)方程;
的方程化為直角坐標(biāo)方程;
(Ⅱ)設(shè)l與圓![]() 相交于
相交于![]() 兩點,求點
兩點,求點![]() 到
到![]() 兩點的距離之積.
兩點的距離之積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場舉行節(jié)日促銷活動,消費滿一定數(shù)額即可獲得一次抽獎機(jī)會,抽獎這可以從以下兩種方式中任選一種進(jìn)行抽獎.
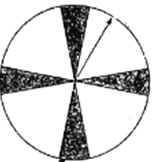
抽獎方式①:讓抽獎?wù)唠S意轉(zhuǎn)動如圖所示的圓盤,圓盤停止后指針指向陰影部分(圖中四個陰影部分均為扇形,且每個扇形圓心角均為![]() ,邊界忽略不計)即中獎.
,邊界忽略不計)即中獎.
抽獎方式②:讓抽獎?wù)邚难b有3個白球和3個紅球的盒子中一次性摸出2個球(球除顏色外不加區(qū)分),如果摸到的是2個紅球,即中獎.
假如你是抽獎?wù)撸瑸榱俗屩歇劦目赡苄源螅銘?yīng)該選擇哪一種抽獎方式?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】第十二屆全國人民代表大會第五次會議和政協(xié)第十二屆全國委員會第五次會議(簡稱兩會)將分別于2017年3月5日和3月3日在北京開幕.全國兩會召開前夕,某網(wǎng)站推出兩會熱點大型調(diào)查,調(diào)查數(shù)據(jù)表明,民生問題是百姓最為關(guān)心的熱點,參與調(diào)查者中關(guān)注此問題的約占![]() .現(xiàn)從參與者中隨機(jī)選出200人,并將這200人按年齡分組:第
.現(xiàn)從參與者中隨機(jī)選出200人,并將這200人按年齡分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示:
,得到的頻率分布直方圖如圖所示:

(1)現(xiàn)在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取12人,再從這12人中隨機(jī)抽取3人贈送禮品,求抽取的3人中至少有![]() 人年齡在第3組的概率;
人年齡在第3組的概率;
(2)若從所有參與調(diào)查的人(人數(shù)很多)中任意選出3人,記關(guān)注民生問題的人數(shù)為X,求X的分布列與期望;
(3)把年齡在第1,2,3組的居民稱為青少年組,年齡在第4,5組的居民稱為中老年組,若選出的200人中不關(guān)注民生問題的人中老年人有10人,問是否有![]() 的把握認(rèn)為是否關(guān)注民生問題與年齡有關(guān)?
的把握認(rèn)為是否關(guān)注民生問題與年齡有關(guān)?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
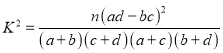 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)是定義在R上的奇函數(shù),且當(dāng)x≥0時, ![]() ,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,則實數(shù)t的取值范圍是. .
,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,則實數(shù)t的取值范圍是. .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義:若函數(shù)y=f(x)在某一區(qū)間D上任取兩個實數(shù)x1、x2 , 且x1≠x2 , 都有 ![]() ,則稱函數(shù)y=f(x)在區(qū)間D上具有性質(zhì)L.
,則稱函數(shù)y=f(x)在區(qū)間D上具有性質(zhì)L.
(1)寫出一個在其定義域上具有性質(zhì)L的對數(shù)函數(shù)(不要求證明).
(2)對于函數(shù) ![]() ,判斷其在區(qū)間(0,+∞)上是否具有性質(zhì)L?并用所給定義證明你的結(jié)論.
,判斷其在區(qū)間(0,+∞)上是否具有性質(zhì)L?并用所給定義證明你的結(jié)論.
(3)若函數(shù) ![]() 在區(qū)間(0,1)上具有性質(zhì)L,求實數(shù)a的取值范圍.
在區(qū)間(0,1)上具有性質(zhì)L,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),在以原點為極點,
為參數(shù)),在以原點為極點, ![]() 軸正半軸為極軸的極坐標(biāo)系中,直線
軸正半軸為極軸的極坐標(biāo)系中,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的傾斜角;
的傾斜角;
(2)設(shè)點![]() ,
, ![]() 和
和![]() 交于
交于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com