
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓的短半軸長為半徑的圓與直線
,以原點為圓心,橢圓的短半軸長為半徑的圓與直線![]() 相切.
相切. ![]() 、
、![]() 是橢圓
是橢圓![]() 的右頂點與上頂點,直線
的右頂點與上頂點,直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點.
兩點.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當四邊形![]() 面積取最大值時,求
面積取最大值時,求![]() 的值.
的值.
 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.曲線
軸正半軸為極軸,建立極坐標系.曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為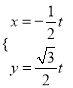 (
(![]() 為參數)
為參數)
(1)求曲線![]() 的直角坐標方程及曲線
的直角坐標方程及曲線![]() 的極坐標方程;
的極坐標方程;
(2)當![]() (
(![]() )時在曲線
)時在曲線![]() 上對應的點為
上對應的點為![]() ,若
,若![]() 的面積為
的面積為![]() ,求
,求![]() 點的極坐標,并判斷
點的極坐標,并判斷![]() 是否在曲線
是否在曲線![]() 上(其中點
上(其中點![]() 為半圓的圓心)
為半圓的圓心)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,過點
,過點![]() 且與
且與![]() 軸垂直的直線為
軸垂直的直線為![]() ,
, ![]() 軸,交
軸,交![]() 于點
于點![]() ,直線
,直線![]() 垂直平分
垂直平分![]() ,交
,交![]() 于點
于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)記點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于不同兩點
交于不同兩點![]() ,且
,且![]() (
(![]() 為常數),直線
為常數),直線![]() 與
與![]() 平行,且與曲線
平行,且與曲線![]() 相切,切點為
相切,切點為![]() ,試問
,試問![]() 的面積是否為定值.若為定值,求出
的面積是否為定值.若為定值,求出![]() 的面積;若不是定值,說明理由.
的面積;若不是定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的首項為
的首項為![]() ,公差為
,公差為![]() ,等比數列
,等比數列![]() 的首項為
的首項為![]() ,公比為
,公比為![]() .
.
(Ⅰ)若數列![]() 的前
的前![]() 項和
項和![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若![]() ,
, ![]() ,且
,且![]() .
.
(i)求![]() 的值;
的值;
(ii)對于數列![]() 和
和![]() ,滿足關系式
,滿足關系式![]() ,
, ![]() 為常數,且
為常數,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018河南安陽市高三一模】如下圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與直線
與直線![]() 之間的陰影部分即為
之間的陰影部分即為![]() ,區域
,區域![]() 中動點
中動點![]() 到
到![]() 的距離之積為1.
的距離之積為1.
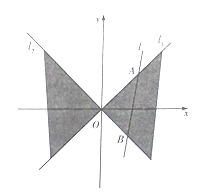
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)動直線![]() 穿過區域
穿過區域![]() ,分別交直線
,分別交直線![]() 于
于![]() 兩點,若直線
兩點,若直線![]() 與軌跡
與軌跡![]() 有且只有一個公共點,求證:
有且只有一個公共點,求證: ![]() 的面積恒為定值.
的面積恒為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,射線OA、OB分別與x軸正半軸成45°和30°角,過點P(1,0)作直線AB分別交OA、OB于A、B兩點,當AB的中點C恰好落在直線y=![]() x上時,求直線AB的方程.
x上時,求直線AB的方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“砥礪奮進的五年”,首都經濟社會發展取得新成就.自2012年以來,北京城鄉居民收入穩步增長.隨著擴大內需,促進消費等政策的出臺,居民消費支出全面增長,消費結構持續優化升級,城鄉居民人均可支配收入快速增長,人民生活品質不斷提升.下圖是北京市2012-2016年城鄉居民人均可支配收入實際增速趨勢圖(例如2012年,北京城鎮居民收入實際增速為![]() ,農村居民收入實際增速為
,農村居民收入實際增速為![]() ).
).
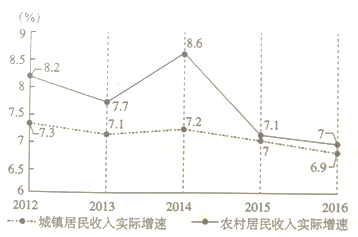
(1)從2012-2016五年中任選一年,求城鎮居民收入實際增速大于![]() 的概率;
的概率;
(2)從2012-2016五年中任選兩年,求至少有一年農村和城鎮居民收入實際增速均超過![]() 的概率;
的概率;
(3)由圖判斷,從哪年開始連續三年農村居民收入實際增速方差最大?(結論不要求證明)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com