
【題目】如圖為某大河的一段支流,岸線![]() 近似滿足
近似滿足![]() ∥
∥![]() 寬度為7
寬度為7![]() 圓
圓![]() 為河中的一個半徑為2
為河中的一個半徑為2![]() 的小島,小鎮
的小島,小鎮![]() 位于岸線
位于岸線![]() 上,且滿足岸線
上,且滿足岸線![]() 現計劃建造一條自小鎮
現計劃建造一條自小鎮![]() 經小島
經小島![]() 至對岸
至對岸![]() 的通道
的通道![]() (圖中粗線部分折線段,
(圖中粗線部分折線段,![]() 在
在![]() 右側),為保護小島,
右側),為保護小島,![]() 段設計成與圓
段設計成與圓![]() 相切,設
相切,設![]()
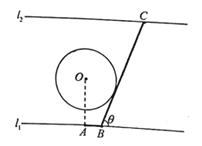
(1)試將通道![]() 的長
的長![]() 表示成
表示成![]() 的函數,并指出其定義域.
的函數,并指出其定義域.
(2)求通道![]() 的最短長.
的最短長.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】技術員小張對甲、乙兩項工作投入時間![]() (小時)與做這兩項工作所得報酬
(小時)與做這兩項工作所得報酬![]() (百元)的關系式為:
(百元)的關系式為:![]() ,若這兩項工作投入的總時間為120小時,且每項工作至少投入20小時.
,若這兩項工作投入的總時間為120小時,且每項工作至少投入20小時.
(1)試建立小張所得總報酬![]() (單位:百元)與對乙項工作投入的時間
(單位:百元)與對乙項工作投入的時間![]() (單位:小時)的函數關系式,并指明函數定義域;
(單位:小時)的函數關系式,并指明函數定義域;
(2)小張如何計劃使用時間,才能使所得報酬最高?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AOB是一塊半徑為r的扇形空地,![]() .某單位計劃在空地上修建一個矩形的活動場地OCDE及一矩形停車場EFGH,剩余的地方進行綠化.若
.某單位計劃在空地上修建一個矩形的活動場地OCDE及一矩形停車場EFGH,剩余的地方進行綠化.若![]() ,設
,設![]()
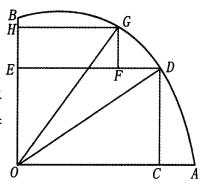
(Ⅰ)記活動場地與停車場占地總面積為![]() ,求
,求![]() 的表達式;
的表達式;
(Ⅱ)當![]() 為何值時,可使活動場地與停車場占地總面積最大.
為何值時,可使活動場地與停車場占地總面積最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,x∈[-1,1],函數
,x∈[-1,1],函數![]() ,a∈R的最小值為h(a).
,a∈R的最小值為h(a).
(1)求h(a)的解析式;
(2)是否存在實數m,n同時滿足下列兩個條件:①m>n>3;②當h(a)的定義域為[n,m]時,值域為[n2,m2]?若存在,求出m,n的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項的和為
項的和為![]() 且
且![]() 數列
數列![]() 滿足
滿足![]() 且對任意正整數
且對任意正整數![]() 都有
都有![]() 成等比數列.
成等比數列.
(1)求數列![]() 的通項公式.
的通項公式.
(2)證明數列![]() 為等差數列.
為等差數列.
(3)令![]() 問是否存在正整數
問是否存在正整數![]() 使得
使得![]() 成等比數列?若存在,求出
成等比數列?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)滿足條件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函數f(x)的解析式;
(2)在區間[﹣1,1]上,y=f(x)的圖象恒在y=2x+m的圖象上方,試確定實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在幾何體![]() 中,
中,![]() ,四邊形
,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() .
.
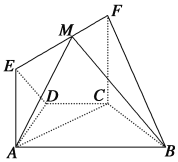
(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上運動,設平面
上運動,設平面![]() 與平面
與平面![]() 所成二面角的平面角為
所成二面角的平面角為![]() ,試求
,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com