
【題目】設函數![]() .
.
(Ⅰ)求![]() 的單調區間;
的單調區間;
(Ⅱ)求![]() 的零點個數;
的零點個數;
(Ⅲ)證明:曲線![]() 沒有經過原點的切線.
沒有經過原點的切線.
【答案】(Ⅰ)![]() 時,
時,![]() 在
在![]() 內單調遞增;
內單調遞增;![]() 時,
時,![]() ,
,![]() ,
,![]() 在區間
在區間![]() 及
及![]() 內單調遞增,在
內單調遞增,在![]() 內單調遞減;(Ⅱ)有且僅有一個零點;(Ⅲ)證明見解析.
內單調遞減;(Ⅱ)有且僅有一個零點;(Ⅲ)證明見解析.
【解析】
試題分析:(Ⅰ)本小題要求單調區間,可先求定義域為![]() ,再求出導數
,再求出導數![]() ,研究
,研究![]() 的根的情況,從而得出
的根的情況,從而得出![]() 的解集,得單調區間;(Ⅱ)函數
的解集,得單調區間;(Ⅱ)函數![]() 的零點個數,可利用(Ⅰ)的單調性證明,如當
的零點個數,可利用(Ⅰ)的單調性證明,如當![]() 時,
時,![]() 在
在![]() 內單調遞增,最多只有1個零點,如能說明函數有正有負,則一定有一個零點;當
內單調遞增,最多只有1個零點,如能說明函數有正有負,則一定有一個零點;當![]() 時,
時,![]() 在
在![]() 及
及![]() 內單調遞增,在
內單調遞增,在![]() 內單調遞減,
內單調遞減,![]() 是
是![]() 的根,要討論
的根,要討論![]() 的正負,從而確定零點個數;(Ⅲ)用反證,假設曲線
的正負,從而確定零點個數;(Ⅲ)用反證,假設曲線![]() 在點
在點![]() 處的切線經過原點,則有
處的切線經過原點,則有![]() ,化簡得
,化簡得![]() .下面只要證明此方程無解即可,可求函數
.下面只要證明此方程無解即可,可求函數![]()
![]() 的最小值,證得結論.
的最小值,證得結論.
試題解析:(Ⅰ)![]() 的定義域為
的定義域為![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
當![]() ,即
,即![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 內單調遞增.
內單調遞增.
當![]() ,即
,即![]() 時,由
時,由![]() 解得,
解得,
![]() ,
,![]() ,且
,且![]() ,
,
在區間![]() 及
及![]() 內,
內,![]() ,在
,在![]() 內,
內,![]() ,
,
∴![]() 在區間
在區間![]() 及
及![]() 內單調遞增,在
內單調遞增,在![]() 內單調遞減.
內單調遞減.
(Ⅱ)由(Ⅰ)可知,當![]() 時,
時,![]() 在
在![]() 內單調遞增,
內單調遞增,
∴![]() 最多只有一個零點.
最多只有一個零點.
又∵![]() ,∴當
,∴當![]() 且
且![]() 時,
時,![]() ;
;
當![]() 且
且![]() 時,
時,![]() ,故
,故![]() 有且僅有一個零點.
有且僅有一個零點.
當![]() 時,∵
時,∵![]() 在
在![]() 及
及![]() 內單調遞增,在
內單調遞增,在![]() 內單調遞減,
內單調遞減,
且![]() ,
,
![]() ,
,
而![]() ,
,
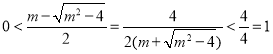 (∵
(∵![]() ),
),
∴![]() ,由此知
,由此知![]() ,
,
又∵當![]() 且
且![]() 時,
時,![]() ,故
,故![]() 在
在![]() 內有且僅有一個零點.
內有且僅有一個零點.
綜上所述,當![]() 時,
時,![]() 有且僅有一個零點.
有且僅有一個零點.
(Ⅲ)假設曲線![]() 在點
在點![]() 處的切線經過原點,
處的切線經過原點,
則有![]() ,即
,即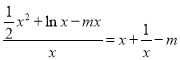 ,
,
化簡得:![]() .(*)
.(*)
記![]() ,則
,則![]() ,
,
令![]() ,解得
,解得![]() .
.
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
∴![]() 是
是![]() 的最小值,即當
的最小值,即當![]() 時,
時,![]() .
.
由此說明方程(*)無解,∴曲線![]() 沒有經過原點的切線.
沒有經過原點的切線.


科目:高中數學 來源: 題型:
【題目】在區間![]() 上,若函數
上,若函數![]() 為增函數,而函數
為增函數,而函數![]() 為減函數,則稱函數
為減函數,則稱函數![]() 為區間
為區間![]() 上的“弱增”函數.則下列函數中,在區間
上的“弱增”函數.則下列函數中,在區間![]() 上不是“弱增”函數的為( )
上不是“弱增”函數的為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設α,β是兩個不同的平面,l是一條直線,以下命題正確的是( )
A.若l⊥α,α⊥β,則lβ
B.若l∥α,α∥β,則lβ
C.若l⊥α,α∥β,則l⊥β
D.若l∥α,α⊥β,則l⊥β
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設平面α∩β=EF,AB⊥α,CD⊥α,垂足分別是B,D,如果增加一個條件,就能推出BD⊥EF,這個條件不可能是下面四個選項中的 ( )
A. AC⊥β
B. AC⊥EF
C. AC與BD在β內的射影在同一條直線上
D. AC與α,β所成的角相等
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com