【題目】下圖是我國2008年至2014年生活垃圾無害化處理量（單位：億噸）的折線圖.
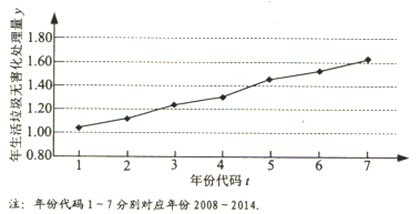
（Ⅰ）由折線圖看出，可用線性回歸模型擬合y與t的關(guān)系，請用相關(guān)系數(shù)加以說明；
（Ⅱ）建立y關(guān)于t的回歸方程（系數(shù)精確到0.01），預測2016年我國生活垃圾無害化處理量.
附注：
參考數(shù)據(jù)：
，
，
，
≈2.646.
參考公式：相關(guān)系數(shù)
回歸方程
中斜率和截距的最小二乘估計公式分別為：
【答案】(Ⅰ)答案見解析；(Ⅱ)答案見解析.
【解析】
試題分析：（Ⅰ）根據(jù)相關(guān)系數(shù)
的公式求出相關(guān)數(shù)據(jù)后，代入公式即可求得的值，最后根據(jù)值的大小回答即可；（Ⅱ）準確求得相關(guān)數(shù)據(jù)，利用最小二乘法建立y關(guān)于t的回歸方程，然后預測．
試題解析：（Ⅰ）由折線圖中數(shù)據(jù)和附注中參考數(shù)據(jù)得
，
，
，
，
.
因為
與
的相關(guān)系數(shù)近似為0.99，說明與的線性相關(guān)相當高，從而可以用線性回歸模型擬合與的關(guān)系.
（Ⅱ）由
及（Ⅰ）得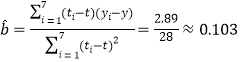
，
.
所以，關(guān)于的回歸方程為：
.
將2016年對應的
代入回歸方程得：
.
所以預測2016年我國生活垃圾無害化處理量將約1.82億噸.
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f(x)=
,下列結(jié)論中錯誤的是
A. 
, f(
)=0
B. 函數(shù)y=f(x)的圖像是中心對稱圖形
C. 若是f(x)的極小值點，則f(x)在區(qū)間（-∞,）單調(diào)遞減
D. 若是f（x）的極值點，則
()=0
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設△ABC的內(nèi)角A，B，C的對邊分別為a，b，c，若c=2 
，sinB=2sinA．
（1）若C= 
，求a，b的值；
（2）若cosC= 
，求△ABC的面積．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】我國古代數(shù)學名著《九章算術(shù)》中的更相減損法的思路與圖相似．執(zhí)行該程序框圖，若輸入的a，b分別為14，18，則輸出的a=（ ） 
A.2
B.4
C.6
D.8
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的短軸長為
，離心率
．
（1）求橢圓
的標準方程；
（2）若
分別是橢圓
的左、右焦點，過
的直線
與橢圓
交于不同的兩點
，求
的內(nèi)切圓半徑的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)f（x）=x（ex﹣1）﹣ax2（e=2.71828…是自然對數(shù)的底數(shù)）．
（1）若 
，求函數(shù)f（x）的單調(diào)區(qū)間；
（2）若f（x）在（﹣1，0）內(nèi)無極值，求a的取值范圍；
（3）設n∈N* ， x＞0，求證： 
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知雙曲線 
與雙曲線 
，給出下列說法，其中錯誤的是（ ）
A.它們的焦距相等
B.它們的焦點在同一個圓上
C.它們的漸近線方程相同
D.它們的離心率相等
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為了解人們對于國家新頒布的“生育二孩放開”政策的熱度，現(xiàn)在某市進行調(diào)查，隨機調(diào)查了50人，他們年齡的頻數(shù)分布及支持“生育二孩”人數(shù)如下表:
年齡 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
頻數(shù) | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二孩放開“政策 | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上統(tǒng)計數(shù)據(jù)填下面2×2列聯(lián)表，并判斷是否有99%的把握認為以45歲為分界點對“生育二孩放開”政策的支持度有差異；
年齡不低于45歲的人數(shù) | 年齡低于45歲的人數(shù) | 合計 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合計 |
(2)若對年齡在[5,15)的被調(diào)查人中隨機選取兩人進行調(diào)查，恰好這兩人都支持“生育二孩放開"政策的概率是多少?
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
附: 
. [導學號113750266]
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f(x)＝－x3＋x2＋b，g(x)＝aln x.
(1)若f(x)在
上的最大值為
，求實數(shù)b的值；
(2)若對任意x∈[1，e]，都有g(shù)(x)≥－x2＋(a＋2)x恒成立，求實數(shù)a的取值范圍．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
