Question

【題目】函數 部分圖象如圖所示.

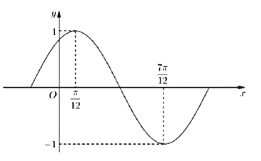
（1）求的最小正周期及解析式；

（2）設，求函數在區間上的最大值和最小值.

Answer 1

【答案】（1） ,；（2）在區間上的最大值為，最小值為．

【解析】

（1）由圖可知A＝1，，從而可求ω；再由圖象經過點（，1），可求得；

（2）依題意g（x）化簡整理為g（x）＝sin（2x），再利用正弦函數的性質結合x的范圍求得g（x）的最大值和最小值．

（1）由圖可知：，A＝1，

∴T＝π，

∴ω2，

∴f（x）＝cos（2x+）

又∵圖象經過點，

∴1＝cos（2），

∴2kπ，k∈Z，

∴2kπ，k∈Z，

又∵||，

∴，

∴解析式為f（x）＝cos（2x）；

（2）g（x）＝f（x）+sin2x

＝cos（2x）+sin2x

＝cos2xcossin2xsin

sin2xcos2x

＝sin（2x）；當時，2x，

當2x時，即x=時，g（x）的最大值為，當2x，即x=時g（x）的最小值為，

綜上所述，在區間上的最大值為，最小值為．