【題目】某企業生產的一種電器的固定成本（即固定投資）為0.5萬元，每生產一臺這種電器還需可變成本（即另增加投資）25元，市場對這種電器的年需求量為5百臺.已知這種電器的銷售收入R與銷售量t的關系可用拋物線表示，如圖.
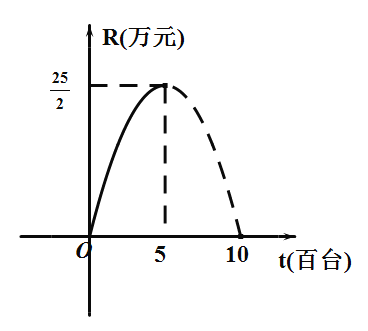
（注：銷售量的單位：百臺，銷售收入與純收益的單位：萬元，生產成本=固定成本+可變成本，精確到1臺和0.01萬元）
（1）寫出銷售收入R與銷售量t之間的函數關系式；
（2）若銷售收入減去生產成本為純收益，寫出純收益與銷售量的函數關系式，并求銷售量是多少時，純收益最大.
科目：高中數學 來源： 題型：
【題目】設三個數
成等差數列，記
對應點的曲線是
.
（1）求曲線的方程；
（2）已知點
，點
，點
，過點
任作直線
與曲線相交于
兩點，設直線
的斜率分別為
，若
，求
滿足的關系式.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法中正確的個數是（ ）
①球的半徑是球面上任意一點與對球心的連線；
②球面上任意兩點的連線是球的直徑；
③用一個平面截一個球，得到的截面是一個圓；
④用一個平面截一個球，得到的截面是一個圓面；
⑤以半圓的直徑所在直線為軸旋轉形成的曲面叫做球；
⑥空間中到定點的距離等于定長的所有的點構成的曲面是球面.
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某地一天從
時的溫度變化曲線近似滿足函數
.
（1）求該地區這一段時間內溫度的最大溫差.
（2）若有一種細菌在
到
之間可以生存，則在這段時間內，該細菌最多能存活多長時間？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】命題p：
x∈R，ax2﹣2ax+1＞0，命題q：指數函數f（x）＝ax（a＞0且a≠1）為減函數，則P是q的（ ）
A.充分不必要條件B.必要不充分條件
C.充分必要條件D.既不充分也不必要條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業甲,乙兩個研發小組,他們研發新產品成功的概率分別為
和
,現安排甲組研發新產品
,乙組研發新產品
.設甲,乙兩組的研發是相互獨立的.
(1)求至少有一種新產品研發成功的概率;
(2)若新產品
研發成功,預計企業可獲得
萬元,若新產品
研發成功,預計企業可獲得利潤
萬元,求該企業可獲得利潤的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】日本數學家角谷靜夫發現的“
猜想”是指：任取一個自然數，如果它是偶數，我們就把它除以
，如果它是奇數我們就把它乘
再加上
，在這樣一個變換下，我們就得到了一個新的自然數。如果反復使用這個變換，我們就會得到一串自然數，猜想就是：反復進行上述運算后，最后結果為，現根據此猜想設計一個程序框圖如圖所示，執行該程序框圖輸入的
，則輸出
值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，一塊長方形區域
，
，
，在邊
的中點
處有一個可轉動的探照燈，其照射角
始終為
，設
，探照燈照射在長方形內部區域的面積為
.
（1）求關于
的函數關系式；
（2）當
時，求的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
