
【題目】已知在等比數列![]() 中,
中, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等差數列.
成等差數列.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)若數列![]() 滿足
滿足![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,試比較
,試比較![]() 與
與![]() 的大小.
的大小.
【答案】(Ⅰ)![]() .(Ⅱ)見解析.
.(Ⅱ)見解析.
【解析】試題分析:(Ⅰ)因為![]() ,所以可根據
,所以可根據![]() ,
, ![]() ,
, ![]() 成等差數列列出關于首公比
成等差數列列出關于首公比![]() 的方程,解得
的方程,解得![]() 的值,即可得到數列
的值,即可得到數列![]() 的通項公式;(Ⅱ)利用(Ⅰ)的結論可得
的通項公式;(Ⅱ)利用(Ⅰ)的結論可得![]() ,根據分組求和法,利用等差數列求和公式以及等比數列求和公式可得
,根據分組求和法,利用等差數列求和公式以及等比數列求和公式可得![]() ,再利用做差法可比較
,再利用做差法可比較![]() 與
與![]() 的大小.
的大小.
試題解析:(Ⅰ)設等比數列![]() 的公比為
的公比為![]() ,∵
,∵![]() ,
, ![]() ,
, ![]() 成等差數列,
成等差數列,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
(Ⅱ)∵![]()
∴![]()
![]()
![]() .
.
因為![]() ,所以
,所以![]()
【方法點晴】本題主要考查等差數列的求和公式及等比數列的求和公式,以及利用“分組求和法”求數列前![]() 項和,屬于中檔題. 利用“分組求和法”求數列前
項和,屬于中檔題. 利用“分組求和法”求數列前![]() 項和常見類型有兩種:一是通項為兩個公比不相等的等比數列的和或差,可以分別用等比數列求和后再相加減;二是通項為一個等差數列和一個等比數列的和或差,可以分別用等差數列求和、等比數列求和后再相加減.
項和常見類型有兩種:一是通項為兩個公比不相等的等比數列的和或差,可以分別用等比數列求和后再相加減;二是通項為一個等差數列和一個等比數列的和或差,可以分別用等差數列求和、等比數列求和后再相加減.


科目:高中數學 來源: 題型:
【題目】事件一:假設某地區有高中生2400人,初中生10900人,小學生11000人.為了了解該地區學生的視力健康狀況,從中抽取![]() 的學生進行調查.事件二:某校為了了解高一年級學生對教師教學的滿意率,打算從高一年級500名學生中抽取50名進行調查.對于事件一和事件二,恰當的抽樣方法分別是( )
的學生進行調查.事件二:某校為了了解高一年級學生對教師教學的滿意率,打算從高一年級500名學生中抽取50名進行調查.對于事件一和事件二,恰當的抽樣方法分別是( )
A. 系統抽樣,分層抽樣
B. 系統抽樣,簡單隨機抽樣
C. 簡單隨機抽樣,系統抽樣
D. 分層抽樣,系統抽樣
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為2,
的棱長為2,![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 上的點,且與頂點不重合.
上的點,且與頂點不重合.
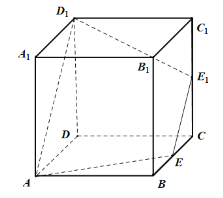
(1)若直線![]() 與
與![]() 相交于點
相交于點![]() ,求證:
,求證:![]() 、
、![]() 、
、![]() 三點共線;
三點共線;
(2)若![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
(ⅰ)求證:幾何體![]() 為棱臺;
為棱臺;
(ⅱ)求棱臺![]() 的體積.
的體積.
(附:棱臺的體積公式![]() ,其中
,其中![]() 、
、![]() 分別為棱臺上下底面積,
分別為棱臺上下底面積,![]() 為棱臺的高)
為棱臺的高)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某音樂院校舉行“校園之星”評選活動,評委由本校全體學生組成,對![]() 兩位選手,隨機調查了20個學生的評分,得到下面的莖葉圖:
兩位選手,隨機調查了20個學生的評分,得到下面的莖葉圖:

所得分數 | 低于60分 | 60分到79分 | 不低于80分 |
分流方向 | 淘汰出局 | 復賽待選 | 直接晉級 |
(1)通過莖葉圖比較![]() 兩位選手所得分數的平均值及分散程度(不要求計算出具體值,得出結論即可);
兩位選手所得分數的平均值及分散程度(不要求計算出具體值,得出結論即可);
(2)舉辦方將會根據評分結果對選手進行三向分流,根據所得分數,估計![]() 兩位選手中哪位選手直接晉級的概率更大,并說明理由.
兩位選手中哪位選手直接晉級的概率更大,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年是中國傳統的農歷“鼠年”,有人用3個圓構成“卡通鼠”的形象,如圖:![]() 是圓Q的圓心,圓Q過坐標原點O;點L、S均在x軸上,圓L與圓S的半徑都等于2,圓S、圓L均與圓Q外切.已知直線l過點O.
是圓Q的圓心,圓Q過坐標原點O;點L、S均在x軸上,圓L與圓S的半徑都等于2,圓S、圓L均與圓Q外切.已知直線l過點O.

(1)若直線l與圓L、圓S均相切,則l截圓Q所得弦長為__________;
(2)若直線l截圓L、圓S、圓Q所得弦長均等于d,則![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方程(2+λ)x-(1+λ)y-2(3+2λ)=0與點P(-2,2).
(1)證明:對任意的實數λ,該方程都表示直線,且這些直線都經過同一定點,并求出這一定點的坐標;
(2)證明:該方程表示的直線與點P的距離d小于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(文)(2017·開封二模)為備戰某次運動會,某市體育局組建了一個由4個男運動員和2個女運動員組成的6人代表隊并進行備戰訓練.
(1)經過備戰訓練,從6人中隨機選出2人進行成果檢驗,求選出的2人中至少有1個女運動員的概率.
(2)檢驗結束后,甲、乙兩名運動員的成績用莖葉圖表示如圖:
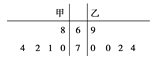
計算說明哪位運動員的成績更穩定.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國明代商人程大位對文學和數學也頗感興趣,他于60歲時完成杰作![]() 直指算法統宗
直指算法統宗![]() ,這是一本風行東亞的數學名著,該書第五卷有問題云:“今有白米一百八十石,令三人從上及和減率分之,只云甲多丙米三十六石,問:各該若干?”翻譯成現代文就是:“今有百米一百八十石,甲乙丙三個人來分,他們分得的米數構成等差數列,只知道甲比丙多分三十六石,那么三人各分得多少米?”請你計算甲應該分得
,這是一本風行東亞的數學名著,該書第五卷有問題云:“今有白米一百八十石,令三人從上及和減率分之,只云甲多丙米三十六石,問:各該若干?”翻譯成現代文就是:“今有百米一百八十石,甲乙丙三個人來分,他們分得的米數構成等差數列,只知道甲比丙多分三十六石,那么三人各分得多少米?”請你計算甲應該分得![]()
![]()
A. 78石 B. 76石 C. 75石 D. 74石
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com