【題目】某小區提倡低碳生活，環保出行，在小區提供自行車出租.該小區有40輛自行車供小區住戶租賃使用，管理這些自行車的費用是每日92元，根據經驗，若每輛自行車的日租金不超過5元，則自行車可以全部出租，若超過5元，則每超過1元，租不出的自行車就增加2輛，為了便于結算，每輛自行車的日租金
元只取整數，用
元表示出租自行車的日純收入（日純收入=一日出租自行車的總收入-管理費用）
（1）求函數的解析式及其定義域；
（2）當租金定為多少時，才能使一天的純收入最大？
【答案】（1）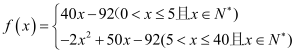
，其定義域為
，（2）定價為12或13，一天的純收入最大，最大值為220元.
【解析】
試題分析：（1）設日租金為
元（
），當
時，一日出租自行車總收入為
元，則此時
，當
時，一日出租自行車總收入為
，則此時
，因此函數
的為分段函數，則函數
的解析式為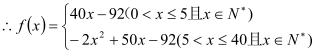
；（2）本問考查求分段函數的最大值，當
且
時，
，函數單調遞增，所以當
時
元，當
且時，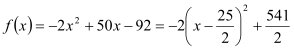 
，根據二次函數圖象及性質可知，當
或13時
，因為220>108，所以函數的最大值為220，此時定價為12或13.
試題解析：（1）由題意：當且時，
當且時，
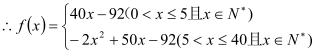
其定義域為
（2）當且時，
當時（元）
當且時，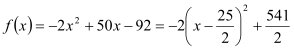
開口向下，對稱軸為
，又
當或13時（元）
當租金定為12元或13元時，
一天的純收入最大為220元
輕松課堂單元測試AB卷系列答案
小題狂做系列答案科目：高中數學 來源： 題型：
【題目】已知函數
（
，
）和函數
（
，
，
）．問：（1）證明：
在
上是增函數；
（2）把函數
和
寫成分段函數的形式，并畫出它們的圖象，總結出
的圖象是如何由
的圖象得到的．請利用上面你的結論說明：
的圖象關于
對稱；
（3）當
，
，
時，若
對于任意的
恒成立，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法錯誤的是（ ）
A．若直線
平面
，直線
平面
，則直線
不一定平行于直線
B．若平面
不垂直于平面
，則
內一定不存在直線垂直于平面
C．若平面
平面
，則
內一定不存在直線平行于平面
D．若平面平面
，平面
平面
，
，則
一定垂直于平面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，圓C的參數方程為
，（t為參數），在以原點O為極點，x軸的非負半軸為極軸建立的極坐標系中，直線
的極坐標方程為
，A，B兩點的極坐標分別為
.
（1）求圓C的普通方程和直線
的直角坐標方程；
（2）點P是圓C上任一點，求△PAB面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以橢圓
：
的中心
為圓心，
為半徑的圓稱為該橢圓的“準圓”.設橢圓
的左頂點為
，左焦點為
，上頂點為
，且滿足
，
.
（1）求橢圓
及其“準圓”的方程；
（2）若橢圓
的“準圓”的一條弦
（不與坐標軸垂直）與橢圓
交于
、
兩點，試證明：當
時，試問弦
的長是否為定值，若是，求出該定值；若不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】梯形ABCD中，AB∥CD，AB平面α，CD平面α，則直線CD與平面α內的直線的位置關系只能是( )
A.平行
B.平行或異面
C.平行或相交
D.異面或相交
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C的對邊分別為a，b，C．已知3cos（B－C）－1＝6cosBcosC．
（1）求cosA；
（2）若a＝3，△ABC的面積為2 
，求b，C．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
,函數
.
（1）求函數
的的單調遞增區間;
（2）設
,問
是否存在極值, 若存在, 請求出極值; 若不存在, 請說明理由;
（3）設
是函數
圖象上任意不同的兩點, 線段
的中點為
,直線的斜率為
.證明:
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】王昌齡《從軍行》兩句詩為“黃沙百戰穿金甲，不破樓蘭終不歸”，其中后一句中“攻破樓蘭”是“返回家鄉”的（ ）
A. 充分條件 B. 必要條件 C. 充要條件 D. 既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com