
【題目】某服裝公司,為確定明年![]() 類服裝的廣告費用,對往年廣告費
類服裝的廣告費用,對往年廣告費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:件)和年利潤
(單位:件)和年利潤![]() (單位:千元)的影響.對2011-2018廣告費
(單位:千元)的影響.對2011-2018廣告費![]() 和年銷售量
和年銷售量![]() 數據進行了處理,分析出以下散點圖和統計量:
數據進行了處理,分析出以下散點圖和統計量:

|
|
|
|
|
|
|
45 | 580 | 2025 | 297 | 1600 | 960 | 1440 |
表中![]()
(1)由散點圖可知,![]() 和
和![]() 更適合作為年銷售量
更適合作為年銷售量![]() 關于年廣告費
關于年廣告費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果和表中數據求![]() 關于
關于![]() 的回歸方程.
的回歸方程.
(3)已知該類服裝年利率![]() 與
與![]() 的關系為
的關系為![]() .由(2)回答以下問題:年廣告費用
.由(2)回答以下問題:年廣告費用![]() 等于60時,年銷售量及年利潤的預報值為多少?年廣告費用為何值時,年利率的預報值最小?
等于60時,年銷售量及年利潤的預報值為多少?年廣告費用為何值時,年利率的預報值最小?
對于一組數據![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,
,![]() ;2.77千元
;2.77千元
【解析】
(1)根據散點圖可判斷哪個更優;
(2)先建立y關于w的線性回歸方程,再求y關于x的回歸方程;
(3)由(2)計算x=60時年銷售量y的預報值和年利潤z的預報值,根據(2) 的結果,利用二次函數的圖象與性質即可得出x為何值時z取得最大值.
(1) 根據散點圖即可得出判斷, ![]() 更適合作為年銷售量
更適合作為年銷售量![]() 關于年廣告費
關于年廣告費![]() 的回歸方程.
的回歸方程.
(2)令![]() ,先建立y關于w的線性回歸方程,
,先建立y關于w的線性回歸方程,
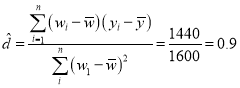 ,
,
![]() ,
,
所以y關于w的線性回歸方程為![]() ,
,
因此y關于x的回歸方程為![]() .
.
(3)當![]() 時,年銷售量y的預報值為
時,年銷售量y的預報值為
![]() (件),
(件),
年利潤z的預報值為
![]() (千元);
(千元);
根據(2)的結果可知,年利潤z的預報值
![]() ,
,
當![]() 千元時,年利率的預報值最小.
千元時,年利率的預報值最小.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
【題目】小趙和小王約定在早上7:00至7:15之間到某公交站搭乘公交車去上學,已知在這段時間內,共有2班公交車到達該站,到站的時間分別為7:05,7:15,如果他們約定見車就搭乘,則小趙和小王恰好能搭乘同一班公交車去上學的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有6本不同的書,在下列不同的條件下,各有多少種不同的分法?
(1)分給甲乙丙三人,其中一個人1本,一個人2本,一個人3本;
(2)分成三組,一組4本,另外兩組各1本;
(3)甲得1本,乙得1本,丙得4本.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某國建了一座時間機器,形似一條圓形地鐵軌道,其上均勻設置了2014個站臺(編號依次為l,2,…,2014)分別對應一個年份,起始站及終點站均為第1站(對應2014年).為節約成本,機器每次運行一圈,只在其中一半的站臺停靠,出于技術原因,每次至多行駛三站必須停靠一次,且所停靠的任兩個站臺不能是圓形軌道的對徑點.試求不同的停靠方式的種數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題,其中正確命題有( )
A.空間任意三個不共面的向量都可以作為一個基底
B.已知向量![]() ,則
,則![]() 與任何向量都不能構成空間的一個基底
與任何向量都不能構成空間的一個基底
C.![]() 是空間四點,若
是空間四點,若![]() 不能構成空間的一個基底,那么
不能構成空間的一個基底,那么![]() 共面
共面
D.已知向量![]() 組是空間的一個基底,若
組是空間的一個基底,若![]() ,則
,則![]() 也是空間的一個基底
也是空間的一個基底
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為坐標原點,動點
為坐標原點,動點![]() 在橢圓
在橢圓![]() :
:![]() 上,該橢圓的左頂點
上,該橢圓的左頂點![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若橢圓![]() 外一點
外一點![]() 滿足,
滿足,![]() 平行于
平行于![]() 軸,
軸,![]() ,動點
,動點![]() 在直線
在直線![]() 上,滿足
上,滿足![]() .設過點
.設過點![]() 且垂直
且垂直![]() 的直線
的直線![]() ,試問直線
,試問直線![]() 是否過定點?若過定點,請寫出該定點,若不過定點請說明理由.
是否過定點?若過定點,請寫出該定點,若不過定點請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC的內切圓分別與邊BC、CA、AB切于點D、E、F,AD與BE交于點P,設點P關于直線EF、FD、DE的對稱點分別X、Y、Z.證明:AX、BY、CZ三線共點.
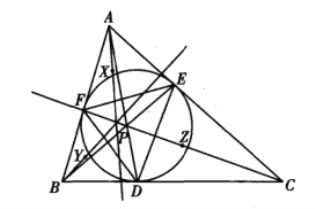
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com