
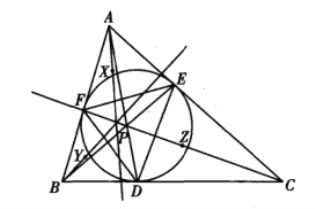
【題目】如圖,△ABC的內切圓分別與邊BC、CA、AB切于點D、E、F,AD與BE交于點P,設點P關于直線EF、FD、DE的對稱點分別X、Y、Z.證明:AX、BY、CZ三線共點.
 全優(yōu)考典單元檢測卷及歸類總復習系列答案
全優(yōu)考典單元檢測卷及歸類總復習系列答案 品學雙優(yōu)卷系列答案
品學雙優(yōu)卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】某服裝公司,為確定明年![]() 類服裝的廣告費用,對往年廣告費
類服裝的廣告費用,對往年廣告費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:件)和年利潤
(單位:件)和年利潤![]() (單位:千元)的影響.對2011-2018廣告費
(單位:千元)的影響.對2011-2018廣告費![]() 和年銷售量
和年銷售量![]() 數(shù)據(jù)進行了處理,分析出以下散點圖和統(tǒng)計量:
數(shù)據(jù)進行了處理,分析出以下散點圖和統(tǒng)計量:

|
|
|
|
|
|
|
45 | 580 | 2025 | 297 | 1600 | 960 | 1440 |
表中![]()
(1)由散點圖可知,![]() 和
和![]() 更適合作為年銷售量
更適合作為年銷售量![]() 關于年廣告費
關于年廣告費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(jù)(1)的判斷結果和表中數(shù)據(jù)求![]() 關于
關于![]() 的回歸方程.
的回歸方程.
(3)已知該類服裝年利率![]() 與
與![]() 的關系為
的關系為![]() .由(2)回答以下問題:年廣告費用
.由(2)回答以下問題:年廣告費用![]() 等于60時,年銷售量及年利潤的預報值為多少?年廣告費用為何值時,年利率的預報值最小?
等于60時,年銷售量及年利潤的預報值為多少?年廣告費用為何值時,年利率的預報值最小?
對于一組數(shù)據(jù)![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】把函數(shù)![]() 的圖象上所有點的橫坐標縮小到原來的
的圖象上所有點的橫坐標縮小到原來的![]() 倍(縱坐標不變),再把得到圖象上所有點向右平移
倍(縱坐標不變),再把得到圖象上所有點向右平移![]() 個單位長度,得到函數(shù)
個單位長度,得到函數(shù)![]() 的圖象.則下列命題正確的是( )
的圖象.則下列命題正確的是( )
A.函數(shù)![]() 在區(qū)間
在區(qū)間![]() ,
,![]() 上單調遞減
上單調遞減
B.函數(shù)![]() 在區(qū)間
在區(qū)間![]() ,
,![]() 上單調遞增
上單調遞增
C.函數(shù)![]() 的圖象關于直線
的圖象關于直線![]() ,
,![]() 對稱
對稱
D.函數(shù)![]() 的圖象關于點
的圖象關于點![]() ,
,![]() 對稱
對稱
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某面包店推出一款新面包,每個面包的成本價為![]() 元,售價為
元,售價為![]() 元,該款面包當天只出一爐(一爐至少
元,該款面包當天只出一爐(一爐至少![]() 個,至多
個,至多![]() 個),當天如果沒有售完,剩余的面包以每個
個),當天如果沒有售完,剩余的面包以每個![]() 元的價格處理掉,為了確定這一爐面包的個數(shù),以便利潤最大化,該店記錄了這款新面包最近
元的價格處理掉,為了確定這一爐面包的個數(shù),以便利潤最大化,該店記錄了這款新面包最近![]() 天的日需求量(單位:個),整理得下表:
天的日需求量(單位:個),整理得下表:
日需求量 |
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
(1)根據(jù)表中數(shù)據(jù)可知,頻數(shù)![]() 與日需求量
與日需求量![]() (單位:個)線性相關,求
(單位:個)線性相關,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若該店這款新面包每日出爐數(shù)設定為![]() 個
個
(i)求日需求量為![]() 個時的當日利潤;
個時的當日利潤;
(ii)求這![]() 天的日均利潤.
天的日均利潤.
相關公式: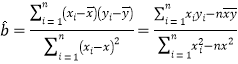 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】[選修4-4:坐標系與參數(shù)方程]
已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,以極點
,以極點![]() 為直角坐標原點,以極軸為
為直角坐標原點,以極軸為![]() 軸的正半軸建立平面直角坐標系
軸的正半軸建立平面直角坐標系![]() ,將曲線
,將曲線![]() 向左平移
向左平移![]() 個單位長度,再將得到的曲線上的每一個點的橫坐標縮短為原來的
個單位長度,再將得到的曲線上的每一個點的橫坐標縮短為原來的![]() ,縱坐標保持不變,得到曲線
,縱坐標保持不變,得到曲線![]()
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,(
,(![]() 為參數(shù)),點
為參數(shù)),點![]() 為曲線
為曲線![]() 上的動點,求點
上的動點,求點![]() 到直線
到直線![]() 距離的最大值.
距離的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若函數(shù)![]() 是
是![]() 上的增函數(shù)求
上的增函數(shù)求![]() 的取值范圍;
的取值范圍;
(2)若函數(shù)![]() 恰有兩個不等的極值點
恰有兩個不等的極值點![]() 、
、![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(2016·重慶高二檢測)如圖,三棱柱ABC-A1B1C1中,側棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中點.
AA1,D是棱AA1的中點.

(1)證明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱為兩部分,求這兩部分體積的比.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com