
【題目】如圖,在六棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正六邊形,
的正六邊形,![]() .
.
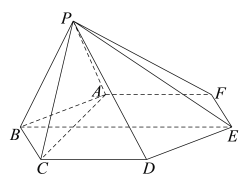
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)要證明面面垂直,需先證明線面垂直,設![]() ,連結
,連結![]() ,根據正六邊形的性質和條件,可證明
,根據正六邊形的性質和條件,可證明![]() 平面
平面![]() ;(2)首先證明
;(2)首先證明![]() ,即
,即![]() 、
、![]() 、
、![]() 兩兩互相垂直,以
兩兩互相垂直,以![]() 、
、![]() 、
、![]() 所在的直線為
所在的直線為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() (如下圖所示),分別求平面
(如下圖所示),分別求平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,根據公式求解
,根據公式求解![]() .
.
解:(1)設![]() ,連結
,連結![]() .
.
在正六邊形![]() 中,根據對稱性
中,根據對稱性![]() 為
為![]() 中點,
中點,
又![]() ,
,![]() ,
,
又因為![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)在正六邊形![]() 中,
中,![]() ,
,
所以![]() ,
,![]() .
.
又因為![]() ,所以
,所以![]() .
.
因為![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 、
、![]() 、
、![]() 兩兩互相垂直.
兩兩互相垂直.
以![]() 、
、![]() 、
、![]() 所在的直線為
所在的直線為![]() 軸、
軸、![]() 軸、
軸、
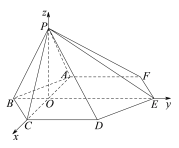
![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() (如圖所示).
(如圖所示).
則![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
設平面![]() 的一個法向量為
的一個法向量為![]() .
.
由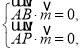 得
得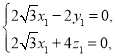 令
令![]() ,解得
,解得![]() ,
,![]() .
.
所以![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() .
.
由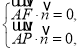 得
得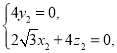 令
令![]() ,解得
,解得![]() .
.
所以![]() .
.
因此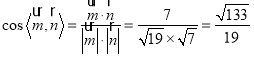 .
.
因為二面角![]() 的平面角為鈍角,
的平面角為鈍角,
故二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
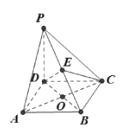
【題目】如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于點
交于點![]() ,
, ![]() 是
是![]() 上任意一點.
上任意一點.
(1)求證: ![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左頂點為
的左頂點為![]() ,右頂點為
,右頂點為![]() ,已知橢圓
,已知橢圓![]() 的離心率為
的離心率為![]() ,且以線段
,且以線段![]() 為直徑的圓被直線
為直徑的圓被直線![]() 所截的弦長為
所截的弦長為![]() .
.
(1)求橢圓的方程;
(2)記橢圓![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點.若線段
兩點.若線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解市民對電視劇市場的愛好,某上星電視臺邀請了100位電視劇愛好者(男50人、女50人)對4月份觀看其播出的電視劇集數進行調研,得到這100名電視劇愛好者觀看集數的中位數為39集(假設這100名電視劇愛好者的觀看集數均在![]() 集內),且觀看集數在
集內),且觀看集數在![]() 集內的人數為15,并根據調查結果畫出如圖所示的頻率分布直方圖.
集內的人數為15,并根據調查結果畫出如圖所示的頻率分布直方圖.

(1)求![]() ,
,![]() 的值;
的值;
(2)有些觀眾喜歡帶有主角光環意識來觀劇.但是最近幾年的影視作品里出現了一個有趣的趨勢——攻氣十足的女性角色越來越討人喜歡,傻白甜的女主們則破了主角光環,各種被嫌棄,更有些劇集中明明是女配的腳本,卻因為更具有大女主氣場,而獲得了比主角更多的關注與聲量,如《完美關系》里的斯黛拉,《精英律師》里的栗娜,《我的前半生》里的唐晶,……已知在這100名電視劇愛好者的女性中有31名認為自己有主角光環意識,男性中有19名認為自己有主角光環意識,根據以上數據請同學們制作出列聯表,并且判斷能否在犯錯誤的概率不超過0.001的前提下認為性別與是否觀劇帶有主角光環意識有關系?
參考公式及數據: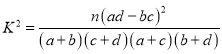 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某度假酒店為了解會員對酒店的滿意度,從中抽取50名會員進行調查,把會員對酒店的“住宿滿意度”與“餐飲滿意度”都分為五個評分標準:1分(很不滿意);2分(不滿意);3分(一般);4分(滿意);5分(很滿意).其統計結果如下表(住宿滿意度為![]() ,餐飲滿意度為
,餐飲滿意度為![]() )
)

(1)求“住宿滿意度”分數的平均數;
(2)求“住宿滿意度”為3分時的5個“餐飲滿意度”人數的方差;
(3)為提高對酒店的滿意度,現從![]() 且
且![]() 的會員中隨機抽取2人征求意見,求至少有1人的“住宿滿意度”為2的概率.
的會員中隨機抽取2人征求意見,求至少有1人的“住宿滿意度”為2的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com