【題目】已知函數
（
是自然對數的底數，
）.
（1）求函數
的單調遞增區間；
（2）若
為整數，
，且當
時，
恒成立，其中
為的導函數，求的最大值.
【答案】（1）當
時，
的增區間為
；當
時，的增區間為
；（2）2.
【解析】
試題分析：（1）求單調增區間，只要解不等式
，它的解集區間就是所求增區間；（2）不等式
恒成立，不等式具體化為
，由于
，因此又可轉化為
，這樣
小于
的最小值，因此下面只要求
的最小值.
，接著要討論
的零點，由于
在
上單調遞增，且
，因此在上有唯一零點，即
在
上存在唯一的零點，設其為
，則
，可證得
為最小值，
，從而整數的最大值為2.
試題解析：（1）
.
若
，則
恒成立，所以，
在區間
上單調遞增.........2分
若
，當
時，，在
上單調遞增.
綜上，當時，的增區間為；當時，的增區間為..... 4分
（2）由于
，所以，
當
時，
，故
————① 6分
令
，則
函數
在上單調遞增，而
所以在上存在唯一的零點，
故在上存在唯一的零點. 8分
設此零點為，則
.
當
時，
；當
時，
；
所以，
在上的最小值為.由
可得
10分
所以，
由于①式等價于
.
故整數的最大值為2. 12分
期末金牌卷系列答案
輕松課堂標準練系列答案科目：高中數學 來源： 題型：
【題目】一個正方體的平面展開圖及該正方體的直觀圖的示意圖如圖所示，在正方體中，設BC的中點為M，GH的中點為N
(1)請將字母F，G，H標記在正方體相應的頂點處（不需說明理由）；
(2)證明：直線MN∥平面BDH
（3）求異面直線MN與AG所成角的余弦值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設F1 ， F2是橢圓 
（0＜b＜2）的左、右焦點，過F1的直線l交橢圓于A，B兩點，若|AF2|+|BF2|最大值為5，則橢圓的離心率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一臺還可以用的機器由于使用的時間較長，它按不同的轉速生產出來的某機械零件有一些會有缺陷，每小時生產有缺陷零件的多少隨機器運轉的速率而變化，下表為抽樣試驗結果：
轉速x（轉/秒） | 16 | 14 | 12 | 8 |
每小時生產有缺陷的零件數y（件） | 11 | 9 | 8 | 5 |
（1）畫出散點圖；
（2）如果y與x有線性相關的關系，求回歸直線方程；
（3）若實際生產中，允許每小時生產的產品中有缺陷的零件最多為10個，那么機器的運轉速度應控制在什么范圍內？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司過去五個月的廣告費支出
與銷售額
（單位：萬元）之間有下列對應數據：
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人員不慎將表格中的第一個數據丟失．已知對呈線性相關關系，且回歸方程為
，則下列說法：①銷售額與廣告費支出正相關；②丟失的數據（表中
處）為30；③該公司廣告費支出每增加1萬元，銷售額一定增加
萬元；④若該公司下月廣告投入8萬元，則銷售
額為70萬元．其中，正確說法有（ ）
A．1個 B．2個 C．3個 D．4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，O為坐標原點，點F為拋物線C1：x2=2py（p＞0）的焦點，且拋物線C1上點M處的切線與圓C2：x2+y2=1相切于點Q．
（Ⅰ）當直線MQ的方程為 
時，求拋物線C1的方程；
（Ⅱ）當正數p變化時，記S1 ， S2分別為△FMQ，△FOQ的面積，求 
的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】極坐標系中橢圓C的方程為ρ2= 
，以極點為原點，極軸為x軸非負半軸，建立平面直角坐標系，且兩坐標系取相同的單位長度．
（1）若橢圓上任一點坐標為P（x，y），求 
的取值范圍；
（2）若橢圓的兩條弦AB，CD交于點Q，且直線AB與CD的傾斜角互補，求證：|QA||QB|=|QC||QD|．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在梯形ABCD中，AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，四邊形BFED為矩形，平面BFED⊥平面ABCD，BF＝1．
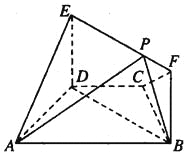
（1）求證：AD⊥平面BFED；
（2）已知點P在線段EF上，
＝2．求三棱錐E－APD的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，已知曲線C1：y=
（x＞0）及曲線C2：y=
(x>0)．C1上的點Pn的橫坐標為an，
過C1上的點Pn(n∈N＋)作直線平行于x軸，交曲線C2于點Qn，再過點Qn作直線平行于y軸，交曲線C1于點Pn＋1.
試求an＋1與an之間的關系，并證明a2n－1<
<a2n(n∈N＋)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com