
已知函數 .
.
(1)若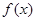 為定義域上的單調函數,求實數m的取值范圍;
為定義域上的單調函數,求實數m的取值范圍;
(2)當m=-1時,求函數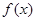 的最大值;
的最大值;
(3)當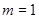 ,
,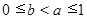 時,證明:
時,證明: .
.
(1)m≥0(2)0(3)構造函數利用導數證明
解析試題分析:(1)由已知得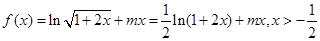 ,
,
所以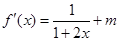 2分
2分
若f(x)在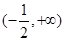 上是增函數,則
上是增函數,則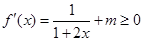 ,即
,即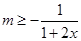 在
在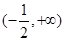 恒成立,
恒成立,
而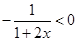 ,故m≥0; 4分
,故m≥0; 4分
若f(x)在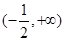 上是減函數,則
上是減函數,則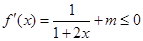 ,即
,即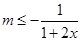 在
在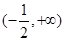 恒成立,
恒成立,
而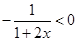 ,故這樣的m不存在. 5分
,故這樣的m不存在. 5分
經檢驗,當m≥0時, 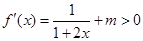 對
對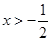 恒成立,
恒成立,
∴當m≥0時,f(x)在定義域上是單調增函數. 6分
(2)當m =-1時, 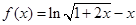 ,則
,則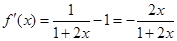 7分
7分
當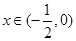 時,
時,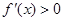 ,此時f(x)為增函數,
,此時f(x)為增函數,
當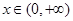 時,
時, 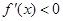 ,此時f(x)為減函數 9分
,此時f(x)為減函數 9分
∴f(x)在x = 0時取得最大值,最大值為0. 10分
(3)當m = 1時,令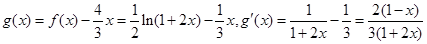 , 11分
, 11分
在[0,1]上總有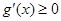 ,即
,即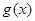 在[0,1]上遞增 , 12分
在[0,1]上遞增 , 12分
∴當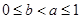 時,
時, ,即
,即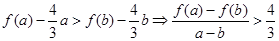 , 13分
, 13分
令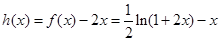 ,由(2)知它在[0,1]上遞減,
,由(2)知它在[0,1]上遞減,
所以當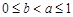 時,
時,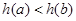 ,即
,即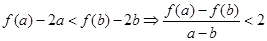 , 14分
, 14分
綜上所述,當m = 1,且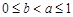 時,
時, . 15分
. 15分
考點:本小題主要考查利用導數研究函數的單調性、極值、最值等和構造函數證明不等式.
點評:導數是研究函數性質的有力工具,利用導數研究函數性質時,不要漏掉函數的定義域,求函數的極值、最值等時最好列表格說明,證明不等式一般要構造函數利用單調性證明問題.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:解答題
已知 ,函數
,函數
(1)求 的極小值;
的極小值;
(2)若 在
在 上為單調增函數,求
上為單調增函數,求 的取值范圍;
的取值范圍;
(3)設 ,若在
,若在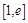 (
( 是自然對數的底數)上至少存在一個
是自然對數的底數)上至少存在一個 ,使得
,使得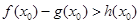 成立,求
成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 (a>0,且a≠1),
(a>0,且a≠1), =
= .
.
(1)函數 的圖象恒過定點A,求A點坐標;
的圖象恒過定點A,求A點坐標;
(2)若函數 的圖像過點(2,
的圖像過點(2, ),證明:函數
),證明:函數 在
在 (1,2)上有唯一的零點.
(1,2)上有唯一的零點.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數
 ,且
,且 能表示成一個奇函數
能表示成一個奇函數 和一個偶函數
和一個偶函數 的和.
的和.
(1)求 和
和 的解析式.
的解析式.
(2)命題 :函數
:函數 在區間
在區間 上是增函數;命題
上是增函數;命題 :函數
:函數 是減函數,如果命題
是減函數,如果命題 、
、 有且僅有一個是真命題,求實數
有且僅有一個是真命題,求實數 的取值范圍.
的取值范圍.
(3)在(2)的條件下,比較 和
和 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com