
【題目】在平面直角坐標(biāo)系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)直線與圓![]() 相切,與橢圓
相切,與橢圓![]() 相交于
相交于![]() 兩點,求證:
兩點,求證:![]() 是定值.
是定值.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】
(1)利用離心率可得![]() ,進(jìn)而得到
,進(jìn)而得到![]() ;將點
;將點![]() 代入橢圓方程可求得
代入橢圓方程可求得![]() ,從而得到橢圓方程;
,從而得到橢圓方程;
(2)①當(dāng)直線![]() 斜率不存在時,可求得
斜率不存在時,可求得![]() 坐標(biāo),從而得到
坐標(biāo),從而得到![]() ,得到
,得到![]() ;②當(dāng)直線
;②當(dāng)直線![]() 斜率存在時,設(shè)直線方程為
斜率存在時,設(shè)直線方程為![]() ,由直線與圓相切可得到
,由直線與圓相切可得到![]() ;將直線方程與橢圓方程聯(lián)立可得到韋達(dá)定理的形式,從而表示出
;將直線方程與橢圓方程聯(lián)立可得到韋達(dá)定理的形式,從而表示出![]() ,整理可得
,整理可得![]() ,得到
,得到![]() ;綜合兩種情況可得到結(jié)論.
;綜合兩種情況可得到結(jié)論.
(1)由題意得:![]() ,即
,即![]()
![]()
![]() 橢圓方程為
橢圓方程為![]()
將![]() 代入橢圓方程得:
代入橢圓方程得:![]()
![]()
![]() 橢圓
橢圓![]() 的方程為:
的方程為:![]()
(2)①當(dāng)直線![]() 斜率不存在時,
斜率不存在時,![]() 方程為:
方程為:![]() 或
或![]()
當(dāng)![]() 時,
時,![]() ,
,![]() ,此時
,此時![]()
![]()
![]()
當(dāng)![]() 時,同理可得
時,同理可得![]()
②當(dāng)直線![]() 斜率存在時,設(shè)
斜率存在時,設(shè)![]() 方程為:
方程為:![]() ,即
,即![]()
![]() 直線與圓相切
直線與圓相切 ![]() ,即
,即![]()
聯(lián)立 得:
得:![]()
設(shè)![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
代入![]() 整理可得:
整理可得:![]()
![]()
![]()
綜上所述:![]() 為定值
為定值![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】世界衛(wèi)生組織的最新研究報告顯示,目前中國近視患者人數(shù)多達(dá)6億,高中生和大學(xué)生的近視率均已超過七成,為了研究每周累計戶外暴露時間(單位:小時)與近視發(fā)病率的關(guān)系,對某中學(xué)一年級200名學(xué)生進(jìn)行不記名問卷調(diào)查,得到如下數(shù)據(jù):
每周累積戶外暴露時間(單位:小時) |
|
|
|
| 不少于28小時 |
近視人數(shù) | 21 | 39 | 37 | 2 | 1 |
不近視人數(shù) | 3 | 37 | 52 | 5 | 3 |
(1)在每周累計戶外暴露時間不少于28小時的4名學(xué)生中,隨機(jī)抽取2名,求其中恰有一名學(xué)生不近視的概率;
(2)若每周累計戶外暴露時間少于14個小時被認(rèn)證為“不足夠的戶外暴露時間”,根據(jù)以上數(shù)據(jù)完成如下列聯(lián)表,并根據(jù)(2)中的列聯(lián)表判斷能否在犯錯誤的概率不超過0.01的前提下認(rèn)為不足夠的戶外暴露時間與近視有關(guān)系?
近視 | 不近視 | |
足夠的戶外暴露時間 | ||
不足夠的戶外暴露時間 |
附:![]()
P | 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點, ![]() 軸為極軸建立極坐標(biāo)系,曲線
軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若曲線![]() 和曲線
和曲線![]() 有三個公共點,求以這三個公共點為頂點的三角形的面積.
有三個公共點,求以這三個公共點為頂點的三角形的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,已知橢圓C:![]() =1(a>b>0)的左右焦點分別為F1,F2,焦距為2,一條準(zhǔn)線方程為x=2.P為橢圓C上一點,直線PF1交橢圓C于另一點Q.
=1(a>b>0)的左右焦點分別為F1,F2,焦距為2,一條準(zhǔn)線方程為x=2.P為橢圓C上一點,直線PF1交橢圓C于另一點Q.
(1)求橢圓C的方程;
(2)若點P的坐標(biāo)為(0,b),求過點P,Q,F2三點的圓的方程;
(3)若![]() =
=![]() ,且λ∈[
,且λ∈[![]() ],求
],求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若在區(qū)間![]() 上存在不相等的實數(shù)
上存在不相等的實數(shù)![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)若函數(shù)![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】每年六、七月份,我國長江中下游地區(qū)進(jìn)入持續(xù)25天左右的梅雨季節(jié),如圖是江南某地區(qū)![]() 年10年間梅雨季節(jié)的降雨量
年10年間梅雨季節(jié)的降雨量![]() 單位:
單位:![]() 的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:
的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:
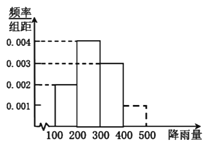
![]() 假設(shè)每年的梅雨季節(jié)天氣相互獨立,求該地區(qū)未來三年里至少有兩年梅雨季節(jié)的降雨量超過350mm的概率.
假設(shè)每年的梅雨季節(jié)天氣相互獨立,求該地區(qū)未來三年里至少有兩年梅雨季節(jié)的降雨量超過350mm的概率.
![]() 老李在該地區(qū)承包了20畝土地種植楊梅,他過去種植的甲品種楊梅,平均每年的總利潤為28萬元
老李在該地區(qū)承包了20畝土地種植楊梅,他過去種植的甲品種楊梅,平均每年的總利潤為28萬元![]() 而乙品種楊梅的畝產(chǎn)量
而乙品種楊梅的畝產(chǎn)量![]() 畝
畝![]() 與降雨量之間的關(guān)系如下面統(tǒng)計表所示,又知乙品種楊梅的單位利潤為
與降雨量之間的關(guān)系如下面統(tǒng)計表所示,又知乙品種楊梅的單位利潤為![]() 元
元![]() ,請你幫助老李分析,他來年應(yīng)該種植哪個品種的楊梅可以使總利潤
,請你幫助老李分析,他來年應(yīng)該種植哪個品種的楊梅可以使總利潤![]() 萬元
萬元![]() 的期望更大?并說明理由.
的期望更大?并說明理由.
降雨量 |
|
|
|
|
畝產(chǎn)量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在數(shù)列 ![]() 中,已知
中,已知 ![]() ,
,![]() 為常數(shù).
為常數(shù).
(1)證明: ![]() 成等差數(shù)列;
成等差數(shù)列;
(2)設(shè) ![]() ,求數(shù)列
,求數(shù)列![]() 的前n項和
的前n項和 ![]() ;
;
(3)當(dāng)![]() 時,數(shù)列
時,數(shù)列 ![]() 中是否存在不同的三項
中是否存在不同的三項![]() 成等比數(shù)列,
成等比數(shù)列,
且![]() 也成等比數(shù)列?若存在,求出
也成等比數(shù)列?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知兩點![]() 、
、![]() ,點
,點![]() 是直角坐標(biāo)平面上的動點,若將點
是直角坐標(biāo)平面上的動點,若將點![]() 的橫坐標(biāo)保持不變、縱坐標(biāo)擴(kuò)大到
的橫坐標(biāo)保持不變、縱坐標(biāo)擴(kuò)大到![]() 倍后得到點
倍后得到點![]() ,且滿足
,且滿足![]() .
.
(1)求動點![]() 所在曲線
所在曲線![]() 的方程;
的方程;
(2)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 、
、![]() 兩點,且滿足
兩點,且滿足![]() ,又點
,又點![]() 關(guān)于原點
關(guān)于原點![]() 的對稱點為點
的對稱點為點![]() ,求點
,求點![]() 、
、![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com