
【題目】如圖,在正方形ABCD中,AB=2,點E、F分別在邊AB、DC上,M為AD的中點,且 ![]() =0,則△MEF的面積的取值范圍為( )
=0,則△MEF的面積的取值范圍為( ) 
A.![]()
B.[1,2]
C.![]()
D.![]()
【答案】A
【解析】解:在正方形ABCD中,∵AB=2,點E、F分別在邊AB、DC上,M為AD的中點,且 ![]() =0,∴ME⊥MF.
=0,∴ME⊥MF.
設∠FMD=θ,則∠EMA=90°﹣θ,
∵tanθ∈(0,2],且cot(90°﹣θ)= ![]() ∈(0,2],∴
∈(0,2],∴ ![]() ≤tanθ≤2.
≤tanθ≤2.
∵MD=MA=1,∴△MEF的面積S= ![]() MEMF=
MEMF= ![]()
![]()
![]() =
= ![]() =
= ![]() =
= ![]() +
+ ![]() ,
,
令x=tanθ,△MEF的面積S(x)= ![]() +
+ ![]() ,x∈[
,x∈[ ![]() ,2],
,2],
顯然S(x)在[ ![]() ,1]上是減函數(shù),在[1,2]上是增函數(shù),S(1)=1,
,1]上是減函數(shù),在[1,2]上是增函數(shù),S(1)=1,
由于當x= ![]() 時,S(x)=
時,S(x)= ![]() +
+ ![]() =
= ![]() ;當 x=2時,S(x)=
;當 x=2時,S(x)= ![]() ,
,
故S(x)= ![]() +
+ ![]() 在區(qū)間∈[
在區(qū)間∈[ ![]() ,2]上的最小值為1,最大值為
,2]上的最小值為1,最大值為 ![]() ,即1≤S≤
,即1≤S≤ ![]() ,
,
故選:A.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知過點![]() 且離心率為
且離心率為![]() 的橢圓
的橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上.
軸上.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓的左準線與
是橢圓的左準線與![]() 軸的交點,過點
軸的交點,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,記橢圓
兩點,記橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,上下兩個頂點分別為
,上下兩個頂點分別為![]() .當線段
.當線段![]() 的中點落在四邊形
的中點落在四邊形![]() 內(包括邊界)時,求直線
內(包括邊界)時,求直線![]() 斜率的取值范圍.
斜率的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
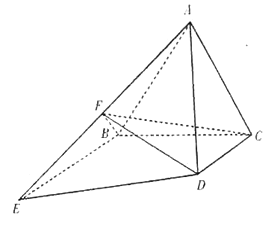
【題目】如圖所示,正三角形![]() 所在平面與梯形
所在平面與梯形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]() ,
, ![]() 為棱
為棱![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“大眾創(chuàng)業(yè),萬眾創(chuàng)新”是李克強總理在本屆政府工作報告中向全國人民發(fā)出的口號.某生產(chǎn)企業(yè)積極響應號召,大力研發(fā)新產(chǎn)品.為了對新研發(fā)的一批產(chǎn)品進行合理定價,將該產(chǎn)品按事先擬定的價格進行試銷,得到一組銷售數(shù)據(jù)![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知變量![]() ,
, ![]() 具有線性相關關系,求產(chǎn)品銷量
具有線性相關關系,求產(chǎn)品銷量![]() (件)關于試銷單價
(件)關于試銷單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(3)用![]() 表示用正確的線性回歸方程得到的與
表示用正確的線性回歸方程得到的與![]() 對應的產(chǎn)品銷量的估計值.當銷售數(shù)據(jù)
對應的產(chǎn)品銷量的估計值.當銷售數(shù)據(jù)![]() 的殘差的絕對值
的殘差的絕對值![]() 時,則將銷售數(shù)據(jù)
時,則將銷售數(shù)據(jù)![]() 稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求抽取的2個銷售數(shù)據(jù)中至少有1個是“好數(shù)據(jù)”的概率.
稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求抽取的2個銷售數(shù)據(jù)中至少有1個是“好數(shù)據(jù)”的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甘肅省瓜州縣自古就以盛產(chǎn)“美瓜”而名揚中外,生產(chǎn)的“瓜州蜜瓜”有4個系列30多個品種,質脆汁多,香甜可口,清爽宜人,含糖量達14%-19%,是消暑止渴的佳品,有詩贊曰:冰泉浸綠玉,霸刀破黃金;涼冷消晚署,清甘洗渴心,調查表明,蜜瓜的甜度與海拔高度、日照時長、溫差有極強的相關性,分別用![]() 表示蜜瓜甜度與海拔高度、日照時長、溫差的相關程度,并對它們進行量化:0表示一般,1表示良,2表示優(yōu),再用綜合指標
表示蜜瓜甜度與海拔高度、日照時長、溫差的相關程度,并對它們進行量化:0表示一般,1表示良,2表示優(yōu),再用綜合指標![]() 的值評定蜜瓜的等級,若
的值評定蜜瓜的等級,若![]() ,則為一級;若
,則為一級;若![]() ,則為二級;若
,則為二級;若![]() ,則為三級.近年來,周邊各省也開始發(fā)展蜜瓜種植,為了了解目前蜜瓜在周邊各省的種植情況,研究人員從不同省份隨機抽取了10塊蜜瓜種植地,得到如下結果:
,則為三級.近年來,周邊各省也開始發(fā)展蜜瓜種植,為了了解目前蜜瓜在周邊各省的種植情況,研究人員從不同省份隨機抽取了10塊蜜瓜種植地,得到如下結果:

(1)若有蜜瓜種植地110塊,試估計等級為一級的蜜瓜種植地的數(shù)量;
(2)在所取樣本的二級和三級蜜瓜種植地中任取2塊, ![]() 表示取到三級蜜瓜種植地的數(shù)量,求隨機變量
表示取到三級蜜瓜種植地的數(shù)量,求隨機變量![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在x= ![]() 取得最大值2,方程f(x)=0的兩個根為x1、x2 , 且|x1﹣x2|的最小值為π.
取得最大值2,方程f(x)=0的兩個根為x1、x2 , 且|x1﹣x2|的最小值為π.
(1)求f(x);
(2)將函數(shù)y=f(x)圖象上各點的橫坐標壓縮到原來的 ![]() ,縱坐標不變,得到函數(shù)y=g(x)的圖象,求函數(shù)g(x)的單調增區(qū)間和在(﹣
,縱坐標不變,得到函數(shù)y=g(x)的圖象,求函數(shù)g(x)的單調增區(qū)間和在(﹣ ![]() ,
, ![]() )上的值域.
)上的值域.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com