【題目】下面給出了2010年亞洲某些國家的國民平均壽命
單位：歲
．
國家 | 平均壽命 | 國家 | 平均壽命 | 國家 | 平均壽命 |
阿曼 |
| 阿富汗 | 59 | 巴基斯坦 |
|
巴林 | | 阿聯酋 |
| 馬來西亞 |
|
朝鮮 |
| 東帝汶 |
| 孟加拉國 |
|
韓國 |
| 柬埔寨 |
| 塞浦路斯 |
|
老撾 |
| 卡塔爾 |
| 沙特阿拉伯 |
|
蒙古 |
| 科威特 | | 哈薩克斯坦 |
|
緬甸 |
| 菲律賓 |
| 印度尼西亞 |
|
日本 |
| 黎巴嫩 |
| 土庫曼斯坦 | 65 |
泰國 |
| 尼泊爾 | 68 | 吉爾吉斯斯坦 |
|
約旦 |
| 土耳其 |
| 烏茲別克斯坦 |
|
越南 | 75 | 伊拉克 |
| 也門 |
|
中國 |
| 以色列 |
| 文萊 |
|
伊朗 | 74 | 新加坡 |
| 敘利亞 |
|
印度 |
|
根據這40個國家的樣本數據，得到如圖所示的頻率分布直方圖，其中樣本數據的分組區間為：
，
，
，
，
，
請根據上述所提供的數據，求出頻率分布直方圖中的a，b；
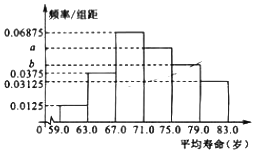
請根據統計思想，利用中的頻率分布直方圖估計亞洲人民的平均壽命及國民壽命的中位數保留一位小數．
舉一反三單元同步過關卷系列答案科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，已知點
，直線
，動直線
垂直
于點
，線段
的垂直平分線交于點
，設點的軌跡為
．
（Ⅰ）求曲線的方程；
（Ⅱ）以曲線上的點
為切點做曲線的切線
，設分別與
、
軸交于
兩點，且恰與以定點
為圓心的圓相切.當圓
的面積最小時，求
與
面積的比．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某高校為調查學生喜歡“應用統計”課程是否與性別有關，隨機抽取了選修課程的60名學生，得到數據如下表：
喜歡統計課程 | 不喜歡統計課程 | 合計 | |
男生 | 20 | 10 | 30 |
女生 | 10 | 20 | 30 |
合計 | 30 | 30 | 60 |
（1）判斷是否有99.5％的把握認為喜歡“應用統計”課程與性別有關？
（2）用分層抽樣的方法從喜歡統計課程的學生中抽取6名學生作進一步調查，將這6名學生作為一個樣本，從中任選3人，求恰有2個男生和1個女生的概率．
下面的臨界值表供參考：
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（參考公式：
，其中
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
為偶函數，且函數
圖象的兩相鄰對稱軸間的距離為
.
（1）求
的值；
（2）將函數的圖象向右平移
個單位后，再將得到的圖象上各點的橫坐標伸長到原來的
倍，縱坐標不變，得到函數
的圖象，求
的單調遞減區間.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lnx﹣ 
x2 ， g（x）= 
x2+x，m∈R，令F（x）=f（x）+g（x）． （Ⅰ）求函數f（x）的單調遞增區間；
（Ⅱ）若關于x的不等式F（x）≤mx﹣1恒成立，求整數m的最小值；
（Ⅲ）若m=﹣1，且正實數x1 ， x2滿足F（x1）=﹣F（x2），求證：x1+x2 
﹣1．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足 an+2﹣an+1=an+1﹣an ， n∈N* ， 且a5= 
若函數f（x）=sin2x+2cos2 
，記yn=f（an），則數列{yn}的前9項和為（ ）
A.O
B.﹣9
C.9
D.1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[2019·牡丹江一中]某校從參加高一年級期末考試的學生中抽取60名學生的成績（均為整數），其成績的頻率分布直方圖如圖所示，由此估計此次考試成績的中位數，眾數和平均數分別是（ ）
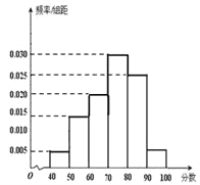
A. 73.3，75，72 B. 73.3，80，73
C. 70，70，76 D. 70，75，75
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
