
【題目】2020年春節突如其來的新型冠狀病毒肺炎在湖北爆發,為了打贏疫情防控阻擊戰,我們執行了延長假期政策,在延長假期面前,我們“停課不停學”,河南省教育廳組織部分優秀學校的優秀教師錄播《名師同步課堂》,我校高一年級要在甲、乙、丙、丁、戊5位數學教師中隨機抽取3人參加錄播課堂,則甲、乙兩位教師同時被選中的概率為( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(x+1)+![]() (a∈R).
(a∈R).
(1)當a=1時,求函數f(x)在點(0,f(0))處的切線方程;
(2)討論函數f(x)的極值;
(3)求證:ln(n+1)> ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汕尾市基礎教育處為調查在校中學生每天放學后的自學時間情況,在本市的所有中學生中隨機抽取了120名學生進行調查,現將日均自學時間小于1小時的學生稱為“自學不足”者![]() 根據調查結果統計后,得到如下
根據調查結果統計后,得到如下![]() 列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為
列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為![]() .
.
非自學不足 | 自學不足 | 合計 | |
配有智能手機 | 30 | ||
沒有智能手機 | 10 | ||
合計 |
![]() 請完成上面的列聯表;
請完成上面的列聯表;
![]() 根據列聯表的數據,能否有
根據列聯表的數據,能否有![]() 的把握認為“自學不足”與“配有智能手機”有關?
的把握認為“自學不足”與“配有智能手機”有關?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的部分圖象大致是( )
的部分圖象大致是( )
A.  B.
B. 
C.  D.
D. 
【答案】D
【解析】當![]() 時,
時, ![]() ,所以去掉A,B;
,所以去掉A,B;
因為![]() ,所以
,所以![]() ,因此去掉C,選D.
,因此去掉C,選D.
點睛:有關函數圖象識別問題的常見題型及解題思路(1)由解析式確定函數圖象的判斷技巧:(1)由函數的定義域,判斷圖象左右的位置,由函數的值域,判斷圖象的上下位置;②由函數的單調性,判斷圖象的變化趨勢;③由函數的奇偶性,判斷圖象的對稱性;④由函數的周期性,判斷圖象的循環往復.(2)由實際情景探究函數圖象.關鍵是將問題轉化為熟悉的數學問題求解,要注意實際問題中的定義域問題.
【題型】單選題
【結束】
8
【題目】《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”,已知某“塹堵”的三視圖如圖所示,則該“塹堵”的外接球的表面積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列![]() 的公比
的公比![]() ,前
,前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.![]() ,
,![]() ,
,![]() 分別是一個等差數列的第1項,第2項,第5項.
分別是一個等差數列的第1項,第2項,第5項.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,
,![]() 的前
的前![]() 項和為
項和為![]() ,且對任意的
,且對任意的![]() 滿足
滿足![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 三個內角
三個內角![]() 所對的邊分別是
所對的邊分別是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圓半徑為2,求
的外接圓半徑為2,求![]() 周長的最大值.
周長的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)由正弦定理將邊角關系化為邊的關系![]() ,再根據余弦定理求角
,再根據余弦定理求角![]() ,(2)先根據正弦定理求邊,用角表示周長,根據兩角和正弦公式以及配角公式化為基本三角函數,最后根據正弦函數性質求最大值.
,(2)先根據正弦定理求邊,用角表示周長,根據兩角和正弦公式以及配角公式化為基本三角函數,最后根據正弦函數性質求最大值.
試題解析:(1)由正弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
因為![]() ,則
,則![]() .
.
(2)由正弦定理![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴周長![]()
![]()
![]()
![]()
![]()
![]()
∵![]() ,∴
,∴![]()
∴當![]() 即
即![]() 時
時![]()
∴當![]() 時,
時, ![]() 周長的最大值為
周長的最大值為![]() .
.
【題型】解答題
【結束】
18
【題目】經調查,3個成年人中就有一個高血壓,那么什么是高血壓?血壓多少是正常的?經國際衛生組織對大量不同年齡的人群進行血壓調查,得出隨年齡變化,收縮壓的正常值變化情況如下表:

其中:  ,
, ![]() ,
, ![]()

(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;(
;(![]() 的值精確到0.01)
的值精確到0.01)
(3)若規定,一個人的收縮壓為標準值的0.9~1.06倍,則為血壓正常人群;收縮壓為標準值的1.06~1.12倍,則為輕度高血壓人群;收縮壓為標準值的1.12~1.20倍,則為中度高血壓人群;收縮壓為標準值的1.20倍及以上,則為高度高血壓人群.一位收縮壓為180mmHg的70歲的老人,屬于哪類人群?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,曲線
,曲線![]() 在
在![]() 處的切線經過點
處的切線經過點![]() .
.
(1)證明: ![]() ;
;
(2)若當![]() 時,
時, 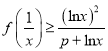 ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:(1)先根據導數幾何意義得切線斜率為![]() ,再根據切線過點
,再根據切線過點![]() ,解得
,解得![]() 導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為
導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為![]() ,分離得
,分離得![]() ,再利用導數求函數
,再利用導數求函數![]() 單調性,利用羅伯特法則求最大值,即得
單調性,利用羅伯特法則求最大值,即得![]() 的取值范圍.
的取值范圍.
試題解析:(1)曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,即
,即![]()
由題意得![]() ,解得
,解得![]()
所以![]()
從而![]()
因為當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() .
.
所以![]() 在區間
在區間![]() 上是減函數,區間
上是減函數,區間![]() 上是增函數,
上是增函數,
從而![]() .
.
(2)由題意知,當![]() 時,
時, ![]() ,所以
,所以![]()
從而當![]() 時,
時, ![]() ,
,
由題意知 ,即
,即![]() ,其中
,其中![]()
設![]() ,其中
,其中![]()
設![]() ,即
,即![]() ,其中
,其中![]()
則![]() ,其中
,其中![]()
(1)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是增函數
是增函數
從而當![]() 時,
時, ![]() ,
,
所以![]() 是增函數,從而
是增函數,從而![]() .
.
故當![]() 時符合題意.
時符合題意.
(2)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,
,
所以![]() 在區間
在區間![]() 上是減函數
上是減函數
從而當![]() 時,
時, ![]()
所以![]() 在
在![]() 上是減函數,從而
上是減函數,從而![]()
故當![]() 時不符合題意.
時不符合題意.
(3)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是減函數
是減函數
從而當![]() 時,
時, ![]()
所以![]() 是減函數,從而
是減函數,從而![]()
故當![]() 時不符合題意
時不符合題意
綜上![]() 的取值范圍是
的取值范圍是![]() .
.
【題型】解答題
【結束】
22
【題目】在直角坐標坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() :
: ![]() .以
.以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸,與直角坐標系
軸的非負半軸為極軸,與直角坐標系![]() 取相同的長度單位,建立極坐標系.
取相同的長度單位,建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() (
(![]() )與曲線
)與曲線![]() 的異于極點的交點為
的異于極點的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示,則下列判斷正確的是( )
的部分圖象如圖所示,則下列判斷正確的是( )
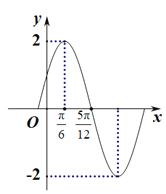
A. 函數的圖象關于點![]() 對稱
對稱
B. 函數的圖象關于直線![]() 對稱
對稱
C. 函數![]() 的最小正周期為
的最小正周期為![]()
D. 當![]() 時,函數
時,函數![]() 的圖象與直線
的圖象與直線![]() 圍成的封閉圖形面積為
圍成的封閉圖形面積為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() 與圓
與圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,點
,點![]() 是線段
是線段![]() 的中點。
的中點。
(1)求直線![]() 的方程;
的方程;
(2)是否存在與直線![]() 平行的直線
平行的直線![]() ,使得
,使得![]() 與與圓
與與圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,
,![]() 不經過點
不經過點![]() ,且
,且![]() 的面積
的面積![]() 最大?若存在,求出
最大?若存在,求出![]() 的方程及對應的
的方程及對應的![]() 的面積S;若不存在,請說明理由。
的面積S;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com