Question

【題目】若直角坐標平面內兩點P，Q滿足條件：①P、Q都在函數y=f（x）的圖象上；②P、Q關于原點對稱，則對稱點（P，Q）是函數y=f（x）的一個“伙伴點組”（點對（P，Q）與（Q，P）看作同一個“伙伴點組”）．則下列函數中，恰有兩個“伙伴點組”的函數是（填空寫所有正確選項的序號）
①y= ；②y= ；③y= ；④y= ．

Answer 1

【答案】②③
【解析】解：①函數y=﹣x﹣1，（x＜0）關于原點對稱的函數為﹣y=x﹣1，即y=﹣x+1，
在x＞0上作出兩個函數的圖象如圖，
由圖象可知兩個函數在x＞0上的交點個數只有一個，所以函數f（x）的“伙伴點組”有1個，不滿足條件．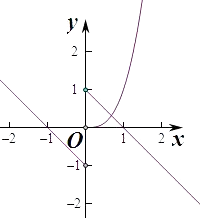

②函數y=﹣ln|x|（x＜0）關于原點對稱的函數為﹣y=﹣ln|﹣x|，即y=ln|x|，
在x＞0上作出兩個函數的圖象如圖，
由圖象可知兩個函數在x＞0上的交點個數有2個，所以函數f（x）的“伙伴點組”有2個，滿足條件．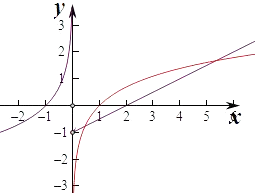

③函數y=﹣x2﹣4x，（x＜0）關于原點對稱的函數為﹣y=﹣x2+4x，即y=x2﹣4x，
在x＞0上作出兩個函數的圖象如圖，
由圖象可知兩個函數在x＞0上的交點個數有2個，所以函數f（x）的“伙伴點組”有2個，滿足條件．

④函數y=e﹣x ， （x＜0）關于原點對稱的函數為﹣y=ex ， 即y=﹣ex ，
在x＞0上作出兩個函數的圖象如圖，
由圖象可知兩個函數在x＞0上的交點個數有0個，所以函數f（x）的“伙伴點組”有0個，不滿足條件．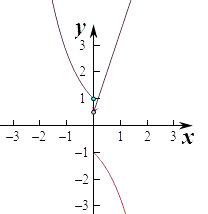
，
所以答案是：②③．
【考點精析】解答此題的關鍵在于理解命題的真假判斷與應用的相關知識，掌握兩個命題互為逆否命題，它們有相同的真假性；兩個命題為互逆命題或互否命題，它們的真假性沒有關系．