【題目】已知函數
.
（1）若曲線
在點
處的切線與直線
垂直，求函數的單調區間；
（2）若對于任意
都有
成立，試求
的取值范圍；
（3）記
.當
時，函數
在區間
上有兩個零點，求實數
的取值范圍。
【答案】（1）單調增區間是
，單調減區間是
.（2）
（3）
【解析】
（1）先由導數的幾何意義求得a，在定義域內，再求出導數大于0的區間，即為函數的增區間，求出導數小于0的區間即為函數的減區間．
（2）根據函數的單調區間求出函數的最小值，要使f（x）＞2（a﹣1）恒成立，需使函數的最小值大于2（a﹣1），從而求得a的取值范圍．
（3）利用導數的符號求出單調區間，再根據函數g（x）在區間[e﹣1，e]上有兩個零點，得到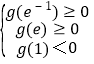
， 解出實數b的取值范圍．
（1）直線
的斜率為1， 函數
)的定義域為
.
因為
，所以
，所以
，
所以
，
.
由
解得
；由
解得
.
所以得單調增區間是，單調減區間是.
（2）
由
解得
；由
解得
.
所以在區間
上單調遞增，在區間
上單調遞減，
所以當
時，函數取得最小值
.
因為對于任意
都有
成立，
所以
即可.
則
，
即
，解得
，
所以
得取值范圍是.
（3）依題意得
，則
，
由
解得
，由
解得
.
所以函數
在區間
上有兩個零點，
所以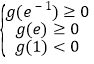
，解得
.
所以
的取值范圍是
.
課時訓練江蘇人民出版社系列答案
黃岡經典趣味課堂系列答案
啟東小題作業本系列答案科目：高中數學 來源： 題型：
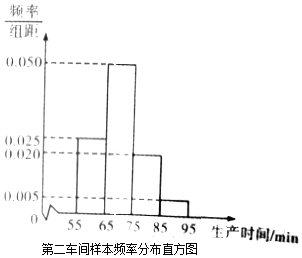
【題目】某工廠有兩個車間生產同一種產品，第一車間有工人200人，第二車間有工人400人，為比較兩個車間工人的生產效率，采用分層抽樣的方法抽取工人，并對他們中每位工人生產完成一件產品的時間（單位：min）分別進行統計，得到下列統計圖表（按照[55，65），[65，75），[75，85），[85，95]分組）．
分組 | 頻數 |
[55，65） | 2 |
[65，75） | 4 |
[75，85） | 10 |
[85，95] | 4 |
合計 | 20 |
第一車間樣本頻數分布表
（Ⅰ）分別估計兩個車間工人中，生產一件產品時間小于75min的人數；
（Ⅱ）分別估計兩車間工人生產時間的平均值，并推測哪個車間工人的生產效率更高？（同一組中的數據以這組數據所在區間中點的值作代表）
（Ⅲ）從第一車間被統計的生產時間小于75min的工人中，隨機抽取3人，記抽取的生產時間小于65min的工人人數為隨機變量X，求X的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一片產量很大的水果種植園，在臨近成熟時隨機摘下某品種水果100個，其質量（均在l至11kg）頻數分布表如下（單位: kg）：
分組 | | | | | |
頻數 | 10 | 15 | 45 | 20 | 10 |
以各組數據的中間值代表這組數據的平均值，將頻率視為概率.
（1）由種植經驗認為，種植園內的水果質量
近似服從正態分布
，其中
近似為樣本平均數
近似為樣本方差
.請估算該種植園內水果質量在
內的百分比；
（2）現在從質量為
的三組水果中用分層抽樣方法抽取14個水果，再從這14個水果中隨機抽取3個．若水果質量的水果每銷售一個所獲得的的利潤分別為2元，4元，6元，記隨機抽取的3個水果總利潤為
元，求的分布列及數學期望.
，則
.查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓
，左、右焦點分別為
，
，右頂點為
，上頂點為
，
為橢圓上在第一象限內一點．
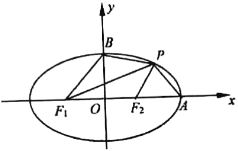
（1）若
．
①求橢圓的離心率
；
②求直線
的斜率．
（2）若
，
，
成等差數列，且
，求直線的斜率的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知各項均為正數的等比數列
的公比
，且
，
是方程
的兩根，記的前n項和為
.
（1）若
，
，
依次成等差數列，求m的值；
（2）設
，數列
的前n項和為
，若
，求n的最小值；
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
