
【題目】如圖,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
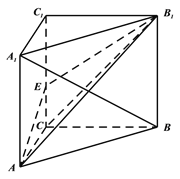
(Ⅰ)證明: ![]() ;
;
(Ⅱ)若![]() ,在棱
,在棱![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ,若存在,求
,若存在,求![]() 的長,若不存在,說明理由.
的長,若不存在,說明理由.
科目:高中數學 來源: 題型:
【題目】某單位計劃在一水庫建一座至多安裝3臺發電機的水電站,過去50年的水文資料顯示,水庫年入流量![]() (年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(1)求未來3年中,設![]() 表示流量超過120的年數,求
表示流量超過120的年數,求![]() 的分布列及期望;
的分布列及期望;
(2)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量![]() 限制,并有如下關系:
限制,并有如下關系:
年入流量 |
|
|
|
發電機最多可運行臺數 | 1 | 2 | 3 |
若某臺發電機運行,則該臺年利潤為5000萬元,若某臺發電機未運行,則該臺年虧損800萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市垃圾處理站每月的垃圾處理量最少為400噸,最多為600噸,月處理成本![]() (元)與月垃圾處理量
(元)與月垃圾處理量![]() (噸)之間的函數關系可近似地表示為
(噸)之間的函數關系可近似地表示為![]() ,且每處理一噸垃圾得到可利用的資源值為100元.
,且每處理一噸垃圾得到可利用的資源值為100元.
(1)該站每月垃圾處理量為多少噸時,才能使每噸垃圾的平均處理成本最低?
(2)該站每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則需要市財政補貼,至少補貼多少元才能使該站不虧損?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若![]() ,證明:函數
,證明:函數![]() 在
在![]() 上單調遞減;
上單調遞減;
(Ⅱ)是否存在實數![]() ,使得函數
,使得函數![]() 在
在![]() 內存在兩個極值點?若存在,求實數
內存在兩個極值點?若存在,求實數![]() 的取值范圍;若不存在,請說明理由. (參考數據:
的取值范圍;若不存在,請說明理由. (參考數據: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為常數,
為常數, ![]() 為自然對數的底數.
為自然對數的底數.
(1)若![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() ,求
,求![]() 的值;
的值;
(2)當![]() 時,判斷方程
時,判斷方程![]() 是否有實根?若無實根請說明理由,若有實根請給出根的個數.
是否有實根?若無實根請說明理由,若有實根請給出根的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】心理學家分析發現視覺和空間能力與性別有關,某數學興趣小組為了驗證這個結論,從興趣小組中按分層抽樣的方法抽取50名同學(男30女20),給所有同學幾何題和代數題各一題,讓各位同學自由選擇一道題進行解答.選題情況如下表:(單位:人)
幾何題 | 代數題 | 總計 | |
男同學 | 22 | 8 | 30 |
女同學 | 8 | 12 | 20 |
總計 | 30 | 20 | 50 |
(Ⅰ)能否據此判斷有97.5%的把握認為視覺和空軍能力與性別有關?
(Ⅱ)經過多次測試后,甲每次解答一道幾何題所用的時間在5—7分鐘,乙每次解答一道幾何題所用的時間在6—8分鐘,現甲、乙各解同一道幾何題,求乙比甲先解答完的概率.
(Ⅲ)現從選擇做幾何題的8名女生中任意抽取兩人對她們的答題情況進行全程研究,記甲、乙兩女生被抽到的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
附表及公式
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
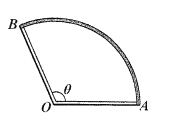
【題目】園林管理處擬在公園某區域規劃建設一半徑為![]() 米,圓心角為
米,圓心角為![]() (弧度)的扇形觀景水池,其中
(弧度)的扇形觀景水池,其中![]() ,
, ![]() 為扇形
為扇形![]() 的圓心,同時緊貼水池周邊(即:
的圓心,同時緊貼水池周邊(即: ![]() 和
和![]() 所對的圓弧)建設一圈理想的無寬度步道.要求總預算費用不超過24萬元,水池造價為每平方米400元,步道造價為每米1000元.
所對的圓弧)建設一圈理想的無寬度步道.要求總預算費用不超過24萬元,水池造價為每平方米400元,步道造價為每米1000元.
(1)若總費用恰好為24萬元,則當![]() 和
和![]() 分別為多少時,可使得水池面積最大,并求出最大面積;
分別為多少時,可使得水池面積最大,并求出最大面積;
(2)若要求步道長為105米,則可設計出的水池最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(2-a)lnx+![]() +2ax.
+2ax.
(1)當a<0時,討論f(x)的單調性;
(2)若對任意的a∈(-3,-2),x1,x2∈[1,3],恒有(m+ln 3)a-2ln 3>|f(x1)-f(x2)|成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com