【題目】已知函數
，其中
為常數， 
為自然對數的底數．
（1）若
在區間
上的最大值為
，求
的值；
（2）當
時，判斷方程
是否有實根？若無實根請說明理由，若有實根請給出根的個數．
【答案】（1）
（2）方程無解
【解析】試題分析：（1）在定義域（0，+∞）內對函數f（x）求導，對a進行分類討論并判斷其單調性，根據f（x）在區間（0，e]上的單調性求其最大值，并判斷其最大值是否為﹣3，若是就可求出相應的最大值．
（2）根據（1）可求出|f（x）|的值域，通過求導可求出函數
的值域，通過比較上述兩個函數的值域，就可判斷出方程
是否有實數解．
試題解析：
（Ⅰ）
， 
， 
①當
時， 
≥0，從而
在
上單調遞增，∴
舍；
②當
時， 
在
上遞增，在
上遞減， 
，令
，得
（Ⅱ）當
時， 
， 
當0<x<1時， 
>0；當x>1時。
<0，∴
是
在定義域
上唯一的極（大）值點，則
∴| 
|≥1，又令
， 
， 
，
∴方程無解．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】若對任意
， 
有唯一確定的
與之對應，則稱
為關于
， 
的二元函數，現定義滿足下列性質的
為關于實數
， 
的廣義“距離”．
（
）非負性： 
，當且僅當
時取等號；
（
）對稱性： 
；
（
）三角形不等式： 
對任意的實數
均成立．
給出三個二元函數：①
；②
；③
，
則所有能夠成為關于
， 
的廣義“距離”的序號為__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等腰梯形
中（如圖1），
， 
， 
為線段
的中點， 
為線段
上的點， 
，現將四邊形
沿
折起（如圖2）．
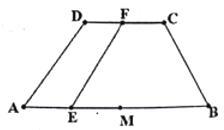
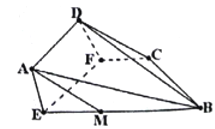
圖1 圖2
⑴求證： 
平面
；
⑵在圖2中，若
，求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著網絡時代的進步，流量成為手機的附帶品，人們可以利用手機隨時隨地的瀏覽網頁，聊天，看視頻，因此，社會上產生了很多低頭族.某研究人員對該地區18∽50歲的5000名居民在月流量的使用情況上做出調查，所得結果統計如下圖所示：
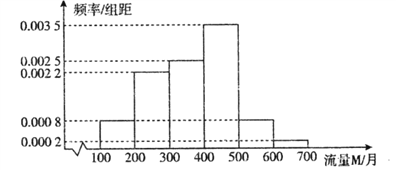
（Ⅰ)以頻率估計概率，若在該地區任取3位居民，其中恰有
位居民的月流量的使用情況
在300M∽400M之間，求
的期望
；
（Ⅱ）求被抽查的居民使用流量的平均值；
（Ⅲ）經過數據分析，在一定的范圍內，流量套餐的打折情況
與其日銷售份數
成線性相關
關系，該研究人員將流量套餐的打折情況
與其日銷售份數
的結果統計如下表所示：
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
銷售份數 | 50 | 85 | 115 | 140 | 160 |
試建立
關于
的的回歸方程.
附注：回歸方程
中斜率和截距的最小二乘估計公式分別為：
， 
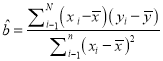查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現有m個（
）實數
，它們滿足下列條件：①
，
②
記這m個實數
的和為
，
即
.
（1）若
，證明： 
；
（2）若m=5，滿足題設條件的5個實數構成數列
.設C為所有滿足題設條件的數列
構成的集合.集合
，求A中所有正數之和；
（3）對滿足題設條件的m個實數構成的兩個不同數列
與
，證明： 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“微信運動”已成為當下熱門的健身方式，小王的微信朋友圈內也有大量好友參與了“微信運動”，他隨機選取了其中的40人（男、女各20人），記錄了他們某一天的走路步數，并將數據整理如下：
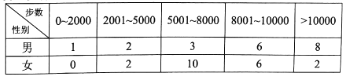
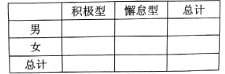
（1）已知某人一天的走路步數超過8000步被系統評定“積極型”，否則為“懈怠型”，根據題意完成下面的
列聯表，并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關？
附：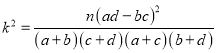 
，
| 0．10 | 0．05 | 0．025 | 0．010 |
| 2．706 | 3．841 | 5．024 | 6．635 |
（2）若小王以這40位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布，現從小王的所有微信好友中任選2人，其中每日走路不超過5000步的有
人，超過10000步的有
人，設
，求
的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4－4：極坐標與參數方程
已知在平面直角坐標系xOy中，O為坐標原點，曲線C：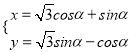 
(α為參數)，在以平面直角坐標系的原點為極點，x軸的正半軸為極軸，取相同單位長度的極坐標系，直線l：ρ
.
(Ⅰ)求曲線C的普通方程和直線l的直角坐標方程；
(Ⅱ)曲線C上恰好存在三個不同的點到直線l的距離相等，分別求出這三個點的極坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如果函數y＝f(x)的導函數的圖象如圖所示，給出下列判斷：
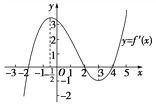
①函數y＝f(x)在區間
內單調遞增；
②函數y＝f(x)在區間
內單調遞減；
③函數y＝f(x)在區間(4,5)內單調遞增；
④當x＝2時，函數y＝f(x)有極小值；
⑤當x＝
時，函數y＝f(x)有極大值．
則上述判斷中正確的是( )
A. ①② B. ②③
C. ③④⑤ D. ③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
