【題目】某網(wǎng)店經(jīng)營各種兒童玩具，該網(wǎng)店老板發(fā)現(xiàn)該店經(jīng)銷的一種手腕可以搖動的
款芭比娃娃玩具在某周內(nèi)所獲純利
（元）與該周每天銷售這種芭比娃娃的個數(shù)
（個）之間的關(guān)系如下表：
每天銷售芭比娃娃個數(shù) | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
該周內(nèi)所獲純利 | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
（1）由表中數(shù)據(jù)可推測
線性相關(guān)，求出回歸直線方程；
（2）請你預測當該店每天銷售這種芭比娃娃20件時，每周獲純利多少？
參考公式：
，
.
【答案】（1）
； （2）大約獲純利多少146元.
【解析】
（1）從散點圖可以看出：這些點大致分布在某一條直線的附近，因此，可以斷定該周內(nèi)所獲純利
與每天銷售這種芭比娃娃的個數(shù)
之間具有線性相關(guān)關(guān)系.求出
，即可求得答；
（2）根據(jù)（1）求得，即可求得答案.
（1）從散點圖可以看出：這些點大致分布在某一條直線的附近，
因此，可以斷定該周內(nèi)所獲純利與每天銷售這種芭比娃娃的個數(shù)之間具有線性相關(guān)關(guān)系.
列出表格如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 66 | 69 | 74 | 81 | 89 | 90 | 91 |
| 198 | 276 | 370 | 486 | 623 | 720 | 819 |
| 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| |||||||
由公式，得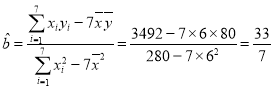
，
.
純利與每天銷售個數(shù)之間的回歸直線方程為.
（2）當
時，
，
因此，當該店每天銷售這種芭比娃娃20件時，每周大約獲純利多少146元.
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
， 
，（其中
， 
為自然對數(shù)的底數(shù)， 
……）.
（1）令
，若
對任意的
恒成立，求實數(shù)
的值；
（2）在（1）的條件下，設
為整數(shù)，且對于任意正整數(shù)
， 
，求
的最小值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（1）討論函數(shù)
的單調(diào)性；
（2）當函數(shù)僅有極小值時，不等實數(shù)
滿足
.證明：
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知某單位甲、乙、丙三個部門的員工人數(shù)分別為24，16，16．現(xiàn)采用分層抽樣的方法從中抽取7人，進行睡眠時間的調(diào)查．
（1）應從甲、乙、丙三個部門的員工中分別抽取多少人？
（2）若抽出的7人中有4人睡眠不足，3人睡眠充足，現(xiàn)從這7人中隨機抽取3人做進一步的身體檢查．用X表示抽取的3人中睡眠充足的員工人數(shù)，求隨機變量X的分布列與數(shù)學期望.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知數(shù)組
，如果數(shù)組
滿足
，且
，其中
，則稱
為
的“兄弟數(shù)組”.
（1）寫出數(shù)組
的“兄弟數(shù)組”
；
（2）若
的“兄弟數(shù)組”是
，試證明：
成等差數(shù)列；
（3）若
為偶數(shù)，且的“兄弟數(shù)組”是，求證：
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下列命題中正確的個數(shù)為（ ）
①“ac＜0”是“二次函數(shù)y＝ax2+bx+c（a，b，c∈R）有兩個異號零點”的必要不充分條件；
②”sinθ
”是“θ
”充分不必要條件；
③“偶函數(shù)的圖象關(guān)于直線x＝0成軸對稱”的逆否命題；
④“若sinx﹣cosx
，則sinx+cosx
的逆命題；
⑤設a，b∈R，則“a＞b”是“a|a|＞b|b|”的充分條件
A.1B.2C.2D.3
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）＝lnx﹣ax+1（a∈R）．
（1）求f（x）的單調(diào)區(qū)間；
（2）設g（x）＝lnx
，若對任意的x1∈（0，+∞），存在x2∈（1，+∞），使得f（x1）＜g（x2）成立，求實數(shù)a的取值范圍．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
