
【題目】已知函數f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的單調區間;
(2)設g(x)=lnx![]() ,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
,若對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求實數a的取值范圍.
【答案】(1)當a≤0時,f(x)單調遞增區間是(0,+∞);當a>0時,f(x)單調遞增區間是(0,![]() ),單調遞減在區間是(
),單調遞減在區間是(![]() ,+∞).(2)a
,+∞).(2)a![]() .
.
【解析】
(1)函數求導得![]() ,然后分a≤0和a>0兩種情況分類求解.
,然后分a≤0和a>0兩種情況分類求解.
(2)根據對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,等價于f(x)max<g(x)max,然后分別求最大值求解即可.
(1)![]() ,
,
當a≤0時,f′(x)>0,f(x)單調遞增,
當a>0時,在區間(0,![]() )上,f′(x)>0,f(x)單調遞增,
)上,f′(x)>0,f(x)單調遞增,
在區間(![]() ,+∞)上,f′(x)<0,f(x)單調遞減.
,+∞)上,f′(x)<0,f(x)單調遞減.
綜上:當a≤0時,f(x)單調遞增區間是(0,+∞),
當a>0時,f(x)單調遞增區間是(0,![]() ),單調遞減在區間是(
),單調遞減在區間是(![]() ,+∞).
,+∞).
(2)![]() ,
,
在區間(1,3)上,g′(x)>0,g(x)單調遞增,
在區間(3,+∞)上,g′(x)<0,g(x)單調遞減,
所以g(x)max=g(3)=ln3![]() ,
,
因為對任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,
等價于f(x)max<g(x)max,
由(1)知當a≤0時,f(x)無最值,
當a>0時,f(x)max=f(![]() )=﹣lna,
)=﹣lna,
所以﹣lna<ln3![]() ,
,
所以![]() ,
,
解得a![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某網店經營各種兒童玩具,該網店老板發現該店經銷的一種手腕可以搖動的![]() 款芭比娃娃玩具在某周內所獲純利
款芭比娃娃玩具在某周內所獲純利![]() (元)與該周每天銷售這種芭比娃娃的個數
(元)與該周每天銷售這種芭比娃娃的個數![]() (個)之間的關系如下表:
(個)之間的關系如下表:
每天銷售芭比娃娃個數 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
該周內所獲純利 | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
(1)由表中數據可推測![]() 線性相關,求出回歸直線方程;
線性相關,求出回歸直線方程;
(2)請你預測當該店每天銷售這種芭比娃娃20件時,每周獲純利多少?
參考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 是某景區的兩條道路(寬度忽略不計,
是某景區的兩條道路(寬度忽略不計,![]() 為東西方向),Q為景區內一景點,A為道路
為東西方向),Q為景區內一景點,A為道路![]() 上一游客休息區,已知
上一游客休息區,已知![]() ,
,![]() (百米),Q到直線
(百米),Q到直線![]() ,
,![]() 的距離分別為3(百米),
的距離分別為3(百米),![]() (百米),現新修一條自A經過Q的有軌觀光直路并延伸至道路
(百米),現新修一條自A經過Q的有軌觀光直路并延伸至道路![]() 于點B,并在B處修建一游客休息區.
于點B,并在B處修建一游客休息區.
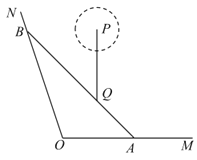
(1)求有軌觀光直路![]() 的長;
的長;
(2)已知在景點Q的正北方6百米的P處有一大型組合音樂噴泉,噴泉表演一次的時長為9分鐘,表演時,噴泉噴灑區域以P為圓心,r為半徑變化,且t分鐘時,![]() (百米)(
(百米)(![]() ,
,![]() ).當噴泉表演開始時,一觀光車S(大小忽略不計)正從休息區B沿(1)中的軌道
).當噴泉表演開始時,一觀光車S(大小忽略不計)正從休息區B沿(1)中的軌道![]() 以
以![]() (百米/分鐘)的速度開往休息區A,問:觀光車在行駛途中是否會被噴泉噴灑到,并說明理由.
(百米/分鐘)的速度開往休息區A,問:觀光車在行駛途中是否會被噴泉噴灑到,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】奇函數f(x)在R上存在導數![]() ,當x<0時,
,當x<0時,![]()
![]() f(x),則使得(x2﹣1)f(x)<0成立的x的取值范圍為( )
f(x),則使得(x2﹣1)f(x)<0成立的x的取值范圍為( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 為
為![]() ,連接
,連接![]() ,
,![]() 得到四棱錐
得到四棱錐![]() (如圖乙),
(如圖乙),![]() 為
為![]() 的中點,
的中點,![]() 是棱
是棱![]() 上一點.
上一點.
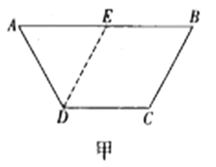
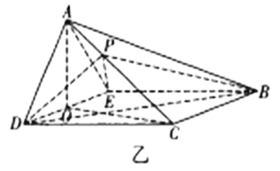
(1)求證:當![]() 為
為![]() 的中點時,平面
的中點時,平面![]() 平面
平面![]() ;
;
(2)是否存在一點![]() ,使平面
,使平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() ,若存在,求
,若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖①中△ABC 為直角三角形![]() D、E 分別為 AB、AC 的中點,將△ADE 沿 DE 折起使平面 ADE⊥BCED,連接 AB,AC,BE如圖②所示.
D、E 分別為 AB、AC 的中點,將△ADE 沿 DE 折起使平面 ADE⊥BCED,連接 AB,AC,BE如圖②所示.
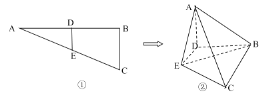
(1)在線段AC上找一點P,使EP∥平面ABD,并求出異面直線AB、EP所成的角;
(2)在平面ABD內找一點Q,使PQ⊥平面ABE,并求三棱錐P-ABE的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com