
【題目】疫情期間,有一批貨物需要用汽車從城市甲運至城市乙,已知從城市甲到城市乙只有兩條公路,且通過這兩條公路所用的時間互不影響.據調查統計,通過這兩條公路從城市甲到城市乙的200輛汽車所用時間的頻數分布如下表:
所用時間 | 10 | 11 | 12 | 13 |
通過公路1的頻數 | 20 | 40 | 20 | 20 |
通過公路2的頻數 | 10 | 40 | 40 | 10 |
(1)為進行某項研究,從所用時間為12的60輛汽車中隨機抽取6輛,若用分層隨機抽樣的方法抽取,求從通過公路1和公路2的汽車中各抽取幾輛:
(2)若從(1)的條件下抽取的6輛汽車中,再任意抽取2輛汽車,求這2輛汽車至少有1輛通過公路1的概率;
(3)假設汽車A只能在約定時間的前11h出發,汽車B只能在約定時間的前12h出發.為了盡最大可能在各自允許的時間內將貨物從城市甲運到城市乙,汽車A和汽車B應如何選擇各自的道路?
【答案】(1)2;4(2)![]() (3)汽車
(3)汽車![]() 應選擇公路1,汽車
應選擇公路1,汽車![]() 應選擇公路2
應選擇公路2
【解析】
(1)由題意,所用時間為12的60輛汽車中,其中公路1有20輛,公路1有40輛,由分層抽樣方法計算可得答案.
(2)由(1)可知抽取的6輛汽車中,通過公路1有2輛用![]() 表示,通過公路1有4輛用
表示,通過公路1有4輛用![]() 表示,列舉出從中任意抽取2輛汽車的情況,可得出這2輛汽車至少有1輛通過公路1的情況,可求出概率.
表示,列舉出從中任意抽取2輛汽車的情況,可得出這2輛汽車至少有1輛通過公路1的情況,可求出概率.
(3)根據題意,設事件![]() 分別表示汽車A在約定時間的前11h出發選擇公路1,2將貨物運往城市乙. 設事件
分別表示汽車A在約定時間的前11h出發選擇公路1,2將貨物運往城市乙. 設事件![]() 分別表示汽車B在約定時間的前12h出發選擇公路1,2將貨物運往城市乙.根據題意求出各自的概率,從而得出答案.
分別表示汽車B在約定時間的前12h出發選擇公路1,2將貨物運往城市乙.根據題意求出各自的概率,從而得出答案.
(1)由題意,所用時間為12天共有60輛汽車,其中公路1有20輛,公路2有40輛.
公路1抽取![]() 輛汽車.
輛汽車.
公路2抽取![]() 輛汽車.
輛汽車.
(2)通過公路1的兩輛汽車分別用![]() 表示,通過公路2的4輛汽車分別用
表示,通過公路2的4輛汽車分別用![]() 表示.
表示.
任意抽取2輛汽車共有如下15種可能結果:
![]()
![]()
![]()
其中至少有1輛經過公路1的有9種.
所以這2輛汽車至少有1輛通過公路1的概率![]() .
.
(3)根據條件,通過這兩條公路從城市甲到城市乙的200輛汽車所用時間的頻率分布如下表.
所用時間 | 10 | 11 | 12 | 13 |
公路1的頻率 | 0.2 | 0.4 | 0.2 | 0.2 |
公路2的頻率 | 0.1 | 0.4 | 0.4 | 0.1 |
設事件![]() 分別表示汽車A在約定時間的前11h出發選擇公路1,2將貨物運往城市乙.
分別表示汽車A在約定時間的前11h出發選擇公路1,2將貨物運往城市乙.
設事件![]() 分別表示汽車B在約定時間的前12h出發選擇公路1,2將貨物運往城市乙.
分別表示汽車B在約定時間的前12h出發選擇公路1,2將貨物運往城市乙.
![]() ,
,![]()
![]()
汽車![]() 應選擇公路1.
應選擇公路1.
![]() ,
,![]()
![]()
汽車![]() 應選擇公路2.
應選擇公路2.


科目:高中數學 來源: 題型:
【題目】2016年入冬以來,各地霧霾天氣頻發,![]() 頻頻爆表(
頻頻爆表(![]() 是指直徑小于或等于
是指直徑小于或等于![]() 微米的顆粒物),各地對機動車更是出臺了各類限行措施,為分析研究車流量與
微米的顆粒物),各地對機動車更是出臺了各類限行措施,為分析研究車流量與![]() 的濃度是否相關,某市現采集周一到周五某一時間段車流量與
的濃度是否相關,某市現采集周一到周五某一時間段車流量與![]() 的數據如下表:
的數據如下表:
時間 | 周一 | 周二 | 周三 | 周四 | 周五 |
車流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
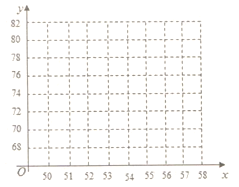
(1)請根據上述數據,在上面給出的坐標系中畫出散點圖;
(2)試判斷![]() 與
與![]() 是否具有線性關系,若有請求出
是否具有線性關系,若有請求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,若沒有,請說明理由;
,若沒有,請說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由國家公安部提出,國家質量監督檢驗檢疫總局發布的《車輛駕駛人員血液、呼氣酒精含量閥值與檢驗標準(GB/T19522-2010)》于2011年7月1日正式實施.車輛駕駛人員酒飲后或者醉酒后駕車血液中的酒精含量閥值見表.經過反復試驗,一般情況下,某人喝一瓶啤酒后酒精在人體血液中的變化規律的“散點圖”見圖,且圖表示的函數模型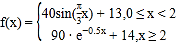 ,則該人喝一瓶啤酒后至少經過多長時間才可以駕車(時間以整小時計算)?(參考數據:
,則該人喝一瓶啤酒后至少經過多長時間才可以駕車(時間以整小時計算)?(參考數據:![]() ,
,![]() )
)
駕駛行為類型 | 閥值 |
飲酒后駕車 |
|
醉酒后駕車 |
|
車輛駕車人員血液酒精含量閥值

喝1瓶啤酒的情況
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:對棱相等的四面體為等腰四面體.
(1)若等腰四面體的每條棱長都是![]() ,求該等腰四面體的體積;
,求該等腰四面體的體積;
(2)求證:等腰四面體每個面的三角形均為銳角三角形:
(3)設等腰四面體![]() 的三個側面與底面所成的角分別為
的三個側面與底面所成的角分別為![]() ,請判斷
,請判斷![]() 是否為定值?如果是定值,請求出該定值;如果不是定值,請說明理由.
是否為定值?如果是定值,請求出該定值;如果不是定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站推出了關于生態文明建設進展情況的調查,大量的統計數據表明,參與調查者中關注此問題的約占80%.現從參與調查的人群中隨機選出![]() 人,并將這
人,并將這![]() 人按年齡分組:第1組
人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示:
,得到的頻率分布直方圖如圖所示:
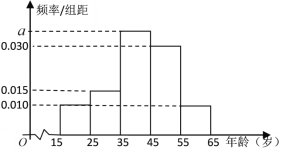
(1)求![]() 的值;
的值;
(2)求出樣本的平均數(同一組數據用該區間的中點值作代表);
(3)現在要從年齡較小的第1,2組中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行問卷調查,求第2組中抽到
人進行問卷調查,求第2組中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知梯形ABCD中,![]() ,如圖(1)所示.現將△ABC沿邊BC翻折至
,如圖(1)所示.現將△ABC沿邊BC翻折至![]() A'BC,記二面角A'—BC—D的大小為θ.
A'BC,記二面角A'—BC—D的大小為θ.
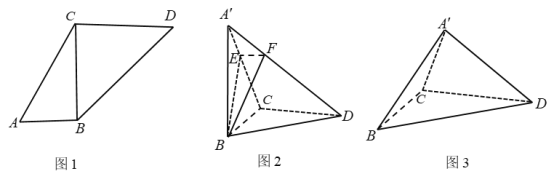
(1)當θ=90°時,如圖(2)所示,過點B作平面與A‘D垂直,分別交![]() 于點E,F,求點E到平面
于點E,F,求點E到平面![]() 的距離;
的距離;
(2)當![]() 時,如圖(3)所示,求二面角
時,如圖(3)所示,求二面角![]() 的正切值
的正切值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com