
【題目】已知動圓![]() 過定點
過定點![]()
![]() ,且與定直線
,且與定直線![]() 相切,動圓圓心
相切,動圓圓心![]() 的軌跡方程為
的軌跡方程為![]() ,直線
,直線![]() 過點
過點![]() 交曲線
交曲線![]() 于
于![]() 兩點.
兩點.
(1)若![]() 交
交![]() 軸于點
軸于點![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 的傾斜角為
的傾斜角為![]() ,在
,在![]() 上是否存在點
上是否存在點![]() 使
使![]() 為正三角形?若能,求點
為正三角形?若能,求點![]() 的坐標;若不能,說明理由.
的坐標;若不能,說明理由.
【答案】(1) ![]() (2) 直線l上不存在點E,使得△ABE是正三角形.
(2) 直線l上不存在點E,使得△ABE是正三角形.
【解析】試題分析:
(1)由題意可知曲線C是拋物線,可得拋物線方程,把直線方程代入拋物線方程得x的一元二次方程,同時設設![]() ,利用韋達定理得
,利用韋達定理得![]() ,用坐標表示出
,用坐標表示出![]() ,利用基本不等式并轉化為
,利用基本不等式并轉化為![]() ,代入韋達定理的結論可得.
,代入韋達定理的結論可得.
(2)假設存在點![]() ,使△ABE為正三角形,則|BE|=|AB|且|AE|=|AB|, 由拋物線定義知
,使△ABE為正三角形,則|BE|=|AB|且|AE|=|AB|, 由拋物線定義知![]() ,這樣把|BE|=
,這樣把|BE|= ![]() 和|AE|=
和|AE|= ![]() 用坐標表示,兩式相減就可解得
用坐標表示,兩式相減就可解得![]() ,從而得E點坐標,但檢驗發現此時
,從而得E點坐標,但檢驗發現此時![]() ,故剛才的解不正確,即不存在E點滿足題意.
,故剛才的解不正確,即不存在E點滿足題意.
試題解析:
(1)依題意,曲線C是以點P為焦點,直線![]() 為準線的拋物線,
為準線的拋物線,
所以曲線C的方程為![]()
設![]() 方程為
方程為![]() 代入
代入![]() 由消去
由消去![]() 得
得![]()
設![]() 、
、![]() ,則
,則![]()
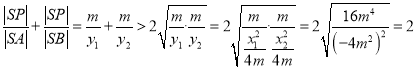
所以![]() 的取值范圍是
的取值范圍是![]()
(2)由(1)知![]() 方程為
方程為![]() 代入
代入![]() 由消去
由消去![]() 得
得![]()
![]() ,
, 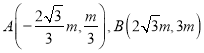
假設存在點![]() ,使△ABE為正三角形,則|BE|=|AB|且|AE|=|AB|,
,使△ABE為正三角形,則|BE|=|AB|且|AE|=|AB|,
![]() 即
即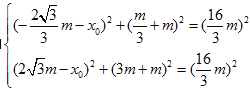 ,
, ![]() .
.
若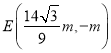 ,則
,則![]()
因此,直線l上不存在點E,使得△ABE是正三角形.
解法二:設AB的中點為G,則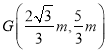
由![]() 聯立
聯立![]() 方程
方程
 與
與![]() 方程求得
方程求得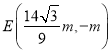
由![]() 得
得![]() ,矛盾
,矛盾
因此,直線l上不存在點E,使得△ABE是正三角形.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人參加了一家公司的招聘面試,面試合格者可正式簽約,甲表示只要面試合格就簽約.乙、丙則約定:兩人面試都合格就一同簽約,否則兩人都不簽約.設每人面試合格的概率都是 ![]() ,且面試是否合格互不影響.求:
,且面試是否合格互不影響.求:
(1)至少有1人面試合格的概率;
(2)簽約人數ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() (a∈R)
(a∈R)
(1)若f(x)在x=0處取得極值,確定a的值,并求此時曲線y=f(x)在點(1,f(1))處的切線方程;
(2)若f(x)在[3,+∞)上為減函數,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義max{a,b}表示實數a,b中的較大的數.已知數列{an}滿足a1=a(a>0),a2=1,an+2= ![]() (n∈N),若a2015=4a,記數列{an}的前n項和為Sn , 則S2015的值為 .
(n∈N),若a2015=4a,記數列{an}的前n項和為Sn , 則S2015的值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+x2﹣xlna(a>0且a≠1)
(1)求函數f(x)在點(0,f(0))處的切線方程;
(2)求函數f(x)單調區間;
(3)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1(e是自然對數的底數),求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,上頂點為
,上頂點為![]() ,焦點為
,焦點為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上異于點
上異于點![]() 的不同的兩點,且滿足直線
的不同的兩點,且滿足直線![]() 與直線
與直線![]() 斜率之積為
斜率之積為![]() .
.
(1)若![]() 為橢圓上不同于長軸端點的任意一點,求
為橢圓上不同于長軸端點的任意一點,求![]() 面積的最大值;
面積的最大值;
(2)試判斷直線![]() 是否過定點;若是,求出定點坐標;若否,請說明理由.
是否過定點;若是,求出定點坐標;若否,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐A﹣BPC中,AP⊥PC,AC⊥BC,M為AB的中點,D為PB的中點,且△PMB為正三角形. 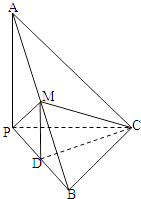
(1)求證:BC⊥平面APC;
(2)若BC=3,AB=10,求三棱錐B﹣MDC的體積VB﹣MDC .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 圖象如圖,
圖象如圖,![]() 是
是![]() 的導函數,則下列數值排序正確的是( )
的導函數,則下列數值排序正確的是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】C
【解析】結合函數的圖像可知過點![]() 的切線的傾斜角最大,過點
的切線的傾斜角最大,過點![]() 的切線的傾斜角最小,又因為點
的切線的傾斜角最小,又因為點![]() 的切線的斜率
的切線的斜率![]() ,點
,點![]() 的切線斜率
的切線斜率![]() ,直線
,直線![]() 的斜率
的斜率![]() ,故
,故![]() ,應選答案C。
,應選答案C。
點睛:本題旨在考查導數的幾何意義與函數的單調性等基礎知識的綜合運用。求解時充分借助題設中所提供的函數圖形的直觀,數形結合進行解答。先將經過兩切點![]() 的直線繞點
的直線繞點![]() 逆時針旋轉到與函數的圖像相切,再將經過兩切點的直線繞點
逆時針旋轉到與函數的圖像相切,再將經過兩切點的直線繞點![]() 順時針旋轉到與函數的圖像相切,這個過程很容易發現
順時針旋轉到與函數的圖像相切,這個過程很容易發現![]() ,從而將問題化為直觀圖形的問題來求解。
,從而將問題化為直觀圖形的問題來求解。
【題型】單選題
【結束】
9
【題目】已知![]() 、
、![]() 為雙曲線
為雙曲線![]() :
:![]() 的左、右焦點,點
的左、右焦點,點![]() 在
在![]() 上,
上,![]() ,則
,則![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面![]() 是不重合的兩個面,下列命題中,所有正確命題的序號是_____.
是不重合的兩個面,下列命題中,所有正確命題的序號是_____.
①若![]() ,
, ![]() 分別是平面
分別是平面![]() 的法向量,則
的法向量,則![]() ;
;
②若![]() ,
, ![]() 分別是平面
分別是平面![]() ,
, ![]() 的法向量,則
的法向量,則![]() ;
;
③若![]() 是平面
是平面![]() 的法向量,
的法向量, ![]() 與
與![]() 共面,則
共面,則![]() ;
;
④若兩個平面的法向量不垂直,則這兩個平面一定不垂直.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com