
【題目】已知函數![]() 有極值,且導函數
有極值,且導函數![]() 的極值點是
的極值點是![]() 的零點。(極值點是指函數取極值時對應的自變量的值)
的零點。(極值點是指函數取極值時對應的自變量的值)
求b關于a的函數關系式,并寫出定義域;
證明:b>3a;
若![]() ,
, ![]() 這兩個函數的所有極值之和不小于
這兩個函數的所有極值之和不小于![]() ,求a的取值范圍。
,求a的取值范圍。
【答案】(1)![]() ,定義域為
,定義域為![]() .(2)見解析(3)
.(2)見解析(3)![]() .
.
【解析】試題分析:(1)先求導函數的極值: ![]() ,再代入原函數得
,再代入原函數得![]() ,化簡可得
,化簡可得![]() ,根據極值存在條件可得
,根據極值存在條件可得![]() ;(2)由(1)得
;(2)由(1)得![]() ,構造函數
,構造函數![]() ,利用導數研究函數單調性,可得
,利用導數研究函數單調性,可得![]() ,即
,即![]() ;(3)先求證
;(3)先求證![]() 的兩個極值之和為零,利用根與系數關系代入化簡即得,再研究導函數極值不小于
的兩個極值之和為零,利用根與系數關系代入化簡即得,再研究導函數極值不小于![]() ,構造差函數
,構造差函數![]() ,利用導數研究其單調性,
,利用導數研究其單調性, ![]() 在
在![]() 上單調遞減.而
上單調遞減.而![]() ,故可得
,故可得![]() 的取值范圍.
的取值范圍.
試題解析:解:(1)由![]() ,得
,得![]() .
.
當![]() 時,
時, ![]() 有極小值
有極小值![]() .
.
因為![]() 的極值點是
的極值點是![]() 的零點.
的零點.
所以![]() ,又
,又![]() ,故
,故![]() .
.
因為![]() 有極值,故
有極值,故![]() 有實根,從而
有實根,從而![]() ,即
,即![]() .
.
![]() 時,
時, ![]() ,故
,故![]() 在R上是增函數,
在R上是增函數, ![]() 沒有極值;
沒有極值;
![]() 時,
時, ![]() 有兩個相異的實根
有兩個相異的實根![]() ,
, ![]() .
.
列表如下
x |
|
|
|
|
|
| + | 0 | – | 0 | + |
|
| 極大值 |
| 極小值 |
|
故![]() 的極值點是
的極值點是![]() .
.
從而![]() ,
,
因此![]() ,定義域為
,定義域為![]() .
.
(2)由(1)知, ![]() .
.
設![]() ,則
,則![]() .
.
當![]() 時,
時, ![]() ,從而
,從而![]() 在
在![]() 上單調遞增.
上單調遞增.
因為![]() ,所以
,所以![]() ,故
,故![]() ,即
,即![]() .
.
因此![]() .
.
(3)由(1)知, ![]() 的極值點是
的極值點是![]() ,且
,且![]() ,
, ![]() .
.
從而![]()
![]()
![]()
記![]() ,
, ![]() 所有極值之和為
所有極值之和為![]() ,
,
因為![]() 的極值為
的極值為![]() ,所以
,所以![]() ,
, ![]() .
.
因為![]() ,于是
,于是![]() 在
在![]() 上單調遞減.
上單調遞減.
因為![]() ,于是
,于是![]() ,故
,故![]() .
.
因此a的取值范圍為![]() .
.
點睛:涉及函數的零點問題、方程解的個數問題、函數圖象的交點個數問題,一般先通過導數研究函數的單調性、最大值、最小值、變化趨勢等,再借助函數的大致圖象判斷零點、方程根、交點的情況,歸根到底還是研究函數的性質,如單調性、極值,然后通過數形結合的思想找到解題的思路.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
【題目】某公司2005~2010年的年利潤x(單位:百萬元)與年廣告支出y(單位:百萬元)的統計資料如表所示:
年份 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
利潤x | 12.2 | 14.6 | 16 | 18 | 20.4 | 22.3 |
支出y | 0.62 | 0.74 | 0.81 | 0.89 | 1 | 1.11 |
根據統計資料,則( )
A.利潤中位數是16,x與y有正線性相關關系
B.利潤中位數是18,x與y有負線性相關關系
C.利潤中位數是17,x與y有正線性相關關系
D.利潤中位數是17,x與y有負線性相關關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C所對的邊分別是a,b,c,已知a=2,c= ![]() ,cosA=﹣
,cosA=﹣ ![]() .
.
(1)求sinC和b的值;
(2)求cos(2A+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(4,3),
=(4,3), ![]() =(2,﹣1),O為坐標原點,P是直線AB上一點.
=(2,﹣1),O為坐標原點,P是直線AB上一點.
(1)若點P是線段AB的中點,求向量 ![]() 與向量
與向量 ![]() 夾角θ的余弦值;
夾角θ的余弦值;
(2)若點P在線段AB的延長線上,且| ![]() |=
|= ![]() |
| ![]() |,求點P的坐標.
|,求點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]在平面坐標系中xOy中,已知直線l的參考方程為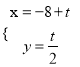 (t為參數),曲線C的參數方程為
(t為參數),曲線C的參數方程為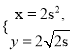 (s為參數)。設p為曲線C上的動點,求點P到直線l的距離的最小值
(s為參數)。設p為曲線C上的動點,求點P到直線l的距離的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱柱ABC﹣A1B1C1的側面AA1C1C為正方形,側面AA1B1B⊥側面BB1C1C,且AC=2,AB= ![]() ,∠A1AB=45°,E、F分別為AA1、CC1的中點.
,∠A1AB=45°,E、F分別為AA1、CC1的中點. 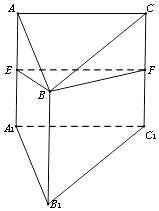
(1)求證:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com