
【題目】某學校研究性學習小組對該校高三學生視力情況進行調查,在高三的全體![]() 名學生中隨機抽取了
名學生中隨機抽取了![]() 名學生的體檢表,并得到如圖的頻率分布直方圖.
名學生的體檢表,并得到如圖的頻率分布直方圖.
年級名次 是否近視 |
|
|
近視 |
|
|
不近視 |
|
|
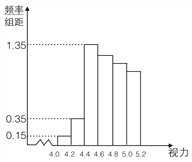
(1)若直方圖中后四組的頻數成等差數列,試估計全年級視力在![]() 以下的人數;
以下的人數;
(2)學習小組成員發現,學習成績突出的學生,近視的比較多,為了研究學生的視力與學習成績是否有關系,對年級名次在![]() 名和
名和![]() 名的學生進行了調查,得到右表中數據,根據表中的數據,能否在犯錯的概率不超過
名的學生進行了調查,得到右表中數據,根據表中的數據,能否在犯錯的概率不超過![]() 的前提下認為視力與學習成績有關系?
的前提下認為視力與學習成績有關系?
(3)在(Ⅱ)中調查的![]() 名學生中,按照分層抽樣在不近視的學生中抽取了
名學生中,按照分層抽樣在不近視的學生中抽取了![]() 人,進一步調查他們良好的護眼習慣,并且在這
人,進一步調查他們良好的護眼習慣,并且在這![]() 人中任取
人中任取![]() 人,記名次在
人,記名次在![]() 的學生人數為
的學生人數為![]() ,求
,求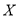 的分布列和數學期望.
的分布列和數學期望.
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
附: 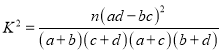
【答案】(1)820;(2) 在犯錯誤的概率不超過![]() 的前提下認為視力與學習成績有關系.(3)答案見解析.
的前提下認為視力與學習成績有關系.(3)答案見解析.
【解析】試題分析:(1)利用直方圖中的前幾個數據和等差數列得到后四組的頻數,再估計其頻率和人數;(2)先利用![]() 公式進行求解,再利用臨界值表進行求解;(3)寫出隨機變量的所有可能取值,利用超幾何分布的概率公式求出相應的概率,再列表得到分布列,進而求出數學期望 .
公式進行求解,再利用臨界值表進行求解;(3)寫出隨機變量的所有可能取值,利用超幾何分布的概率公式求出相應的概率,再列表得到分布列,進而求出數學期望 .
試題解析:(1)由直方圖可知,第一組有3人,第二組有7人,第三組有27人,
因為后四組的頻數成等差數列,所以后四組的頻數依次為27,24,21,18,所以視力
在![]() 以下的頻率為
以下的頻率為![]() ,故全年級視力在
,故全年級視力在![]() 以下的人數約為
以下的人數約為![]() .
.
(2)![]() ,
,
因此在犯錯誤的概率不超過![]() 的前提下認為視力與學習成績有關系.
的前提下認為視力與學習成績有關系.
(3)依題意9人中年級名次在![]() 名和
名和![]() 名分別有3人和6人,
名分別有3人和6人,
![]() 可取0、1、2、3
可取0、1、2、3
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的數學期望
的數學期望![]() .
.


科目:高中數學 來源: 題型:
【題目】某試驗田分別種植了甲乙兩種水稻,為了研究這兩種水稻的產量,抽檢了甲、乙兩種水稻的谷穗各1000株.經統計,得到每株谷穗的粒數的頻率分布直方圖如圖: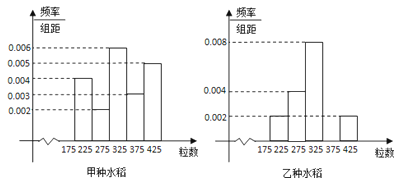
(Ⅰ)求乙種水稻谷穗的粒數落在[325,375)之間的頻率,并將頻率分布直方圖補齊;
(Ⅱ)試根據頻率分布直方圖估計甲種水稻谷穗粒數的中位數與平均數(精確到0.1);
(Ⅲ)根據頻率分布直方圖,請至少從兩方面對甲乙兩種水稻谷穗的粒數作出評價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(x+ ![]() ),
),
(1)判斷并證明函數y=f(x)的奇偶性;
(2)判斷并證明函數y=f(x)在R上的單調性;
(3)當x∈[1,2]時,不等式f(a4x)+f(2x+1)>0恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面內一動點![]() 與兩定點
與兩定點![]() 和
和![]() 連線的斜率之積等于
連線的斜率之積等于![]() .
.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設直線![]() :
: ![]() (
(![]() )與軌跡
)與軌跡![]() 交于
交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() ,當
,當![]() 變化時,求
變化時,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知焦點在x正半軸上,頂點為坐標系原點的拋物線過點A(1,﹣2).
(1)求拋物線的標準方程;
(2)過拋物線的焦點F的直線l與拋物線交于兩點M、N,且△MNO(O為原點)的面積為2 ![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)函數![]() 的圖象能否與
的圖象能否與![]() 軸相切?若能與
軸相切?若能與![]() 軸相切,求實數
軸相切,求實數![]() 的值;否則,請說明理由;
的值;否則,請說明理由;
(2)若函數![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 能取到的最大整數值.
能取到的最大整數值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解高一期末數學考試的情況,從高一的所有學生數學試卷中隨機抽取n份試卷進行成績分析,得到數學成績頻率分布直方圖(如圖所示),其中成績在[50,60)的學生人數為6.
(Ⅰ)求直方圖中x的值;
(Ⅱ)試估計所抽取的數學成績的平均數;
(Ⅲ)試根據樣本估計“該校高一學生期末數學考試成績≥70”的概率.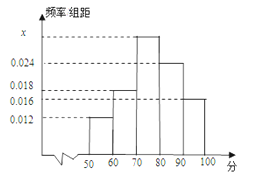
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場一年購進某種貨物900噸,每次都購進x噸,運費為每次9萬元,一年的總存儲費用為9x萬元.
(1)要使一年的總運費與總存儲費用之和最小,則每次購買多少噸?
(2)要使一年的總運費與總存儲費用之和不超過585萬元,則每次購買量在什么范圍?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com