
【題目】某試驗田分別種植了甲乙兩種水稻,為了研究這兩種水稻的產量,抽檢了甲、乙兩種水稻的谷穗各1000株.經統計,得到每株谷穗的粒數的頻率分布直方圖如圖: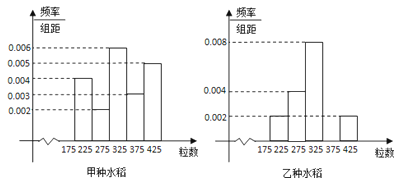
(Ⅰ)求乙種水稻谷穗的粒數落在[325,375)之間的頻率,并將頻率分布直方圖補齊;
(Ⅱ)試根據頻率分布直方圖估計甲種水稻谷穗粒數的中位數與平均數(精確到0.1);
(Ⅲ)根據頻率分布直方圖,請至少從兩方面對甲乙兩種水稻谷穗的粒數作出評價.
【答案】解:(Ⅰ)乙種水稻谷穗的粒數落在[325,375)之間的頻率為1﹣50×(0.002+0.004+0.008+0.002)=0.2,
頻率分布直方圖如圖所示.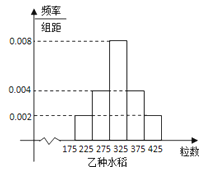
(Ⅱ)設中位數估計值為x,則有 50×(0.004+0.002)+(x﹣275)×0.006=0.5,解得x=308.3
由直方圖得平均數的估計值為50×0.004×200+50×0.002×250+50×0.006×300+50×0.003×350+50×0.005×400=307.5,
答:中位數和平均數的估計值分別為308.3和307.5,
(Ⅲ)由于乙稻谷谷穗粒數平均值的估計值為300<307.5
故可得出結論:乙稻谷谷穗粒數總體上少于甲種水稻,又從頻率分布直方圖可看出乙稻谷谷穗粒數比甲種水稻要整齊.
【解析】(I)根據頻率分布直方圖的小矩形的面積和為1,可求落在[325,375)內的頻率,利用組距為50,求出小矩形的高;
(II)根據中位數的左右兩邊小矩形的面積和相等,求得從左開始面積和為0.5的小矩形底邊橫坐標值,即為中位數;計算各個小矩形的底邊中間值乘以其面積之和,即為數據的平均數;
(III)根據甲、乙兩種水稻谷粒的平均數大小和頻率分布情況說明.
【考點精析】本題主要考查了用樣本的數字特征估計總體的數字特征的相關知識點,需要掌握用樣本估計總體時,如果抽樣的方法比較合理,那么樣本可以反映總體的信息,但從樣本得到的信息會有偏差.在隨機抽樣中,這種偏差是不可避免的才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】【2017江西師范大學附屬中學三模】已知函數![]() 是自然對數的底數).
是自然對數的底數).
(1)求函數![]() 的單調區間;
的單調區間;
(2)若![]() ,當
,當![]() 時,求函數
時,求函數![]() 的最大值;
的最大值;
(3)若![]() 且
且![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出x與銷售額y(單位:萬元)之間有如下對應數據:
P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(Ⅰ)畫出散點圖;
(Ⅱ)求回歸直線方程;
(Ⅲ)試預測廣告費支出為10萬元時,銷售額多大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4—4;坐標系與參數方程)已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,曲線
,曲線![]() 經過平移變換
經過平移變換![]() 得到曲線
得到曲線![]() ;以極點為原點,極軸為
;以極點為原點,極軸為![]() 軸正方向建立平面直角坐標系,直線l的參數方程是
軸正方向建立平面直角坐標系,直線l的參數方程是![]() (
(![]() 為參數).
為參數).
(1)求曲線![]() ,
, ![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線l與曲線![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 的直角坐標為(2,1),若
的直角坐標為(2,1),若![]() ,求直線l的普通方程.
,求直線l的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其質量指標值衡量,并依據質量指標值劃分等級如下表:
質量指標值 |
|
|
|
等級 | 三等品 | 二等品 | 一等品 |
從某企業生產的這種產品中抽取200件,檢測后得到如下的頻率分布直方圖:
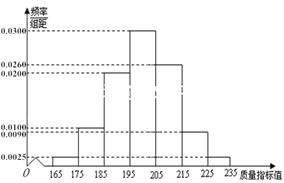
(Ⅰ)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“一、二等品至少要占全部產品92%”的規定?
(Ⅱ)在樣本中,按產品等級用分層抽樣的方法抽取8件,再從這8件產品中隨機抽取4件,求抽取的4件產品中,一、二、三等品都有的概率;
(Ⅲ)該企業為提高產品質量,開展了“質量提升月”活動,活動后再抽樣檢測,產品質量指標值![]() 近似滿足
近似滿足![]() ,則“質量提升月”活動后的質量指標值的均值比活動前大約提升了多少?
,則“質量提升月”活動后的質量指標值的均值比活動前大約提升了多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校研究性學習小組對該校高三學生視力情況進行調查,在高三的全體![]() 名學生中隨機抽取了
名學生中隨機抽取了![]() 名學生的體檢表,并得到如圖的頻率分布直方圖.
名學生的體檢表,并得到如圖的頻率分布直方圖.
年級名次 是否近視 |
|
|
近視 |
|
|
不近視 |
|
|
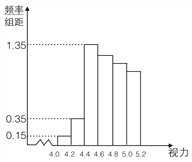
(1)若直方圖中后四組的頻數成等差數列,試估計全年級視力在![]() 以下的人數;
以下的人數;
(2)學習小組成員發現,學習成績突出的學生,近視的比較多,為了研究學生的視力與學習成績是否有關系,對年級名次在![]() 名和
名和![]() 名的學生進行了調查,得到右表中數據,根據表中的數據,能否在犯錯的概率不超過
名的學生進行了調查,得到右表中數據,根據表中的數據,能否在犯錯的概率不超過![]() 的前提下認為視力與學習成績有關系?
的前提下認為視力與學習成績有關系?
(3)在(Ⅱ)中調查的![]() 名學生中,按照分層抽樣在不近視的學生中抽取了
名學生中,按照分層抽樣在不近視的學生中抽取了![]() 人,進一步調查他們良好的護眼習慣,并且在這
人,進一步調查他們良好的護眼習慣,并且在這![]() 人中任取
人中任取![]() 人,記名次在
人,記名次在![]() 的學生人數為
的學生人數為![]() ,求
,求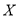 的分布列和數學期望.
的分布列和數學期望.
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
附: 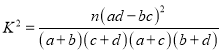
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三國時期趙爽在《勾股方圓圖注》中對勾股定理的證明可用現代數學表述為如圖所示,我們教材中利用該圖作為“( )”的幾何解釋. 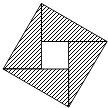
A.如果a>b,b>c,那么a>c
B.如果a>b>0,那么a2>b2
C.對任意實數a和b,有a2+b2≥2ab,當且僅當a=b時等號成立
D.如果a>b,c>0那么ac>bc
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com