
【題目】如圖,多面體 ABCDEF中,四邊形ABCD是邊長為2的菱形,且平面ABCD⊥平面DCE.AF∥DE,且AF=![]() DE=2,BF=2
DE=2,BF=2![]() .
.
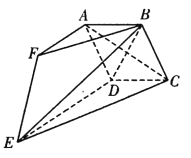
(1)求證:AC⊥BE;
(2)若點(diǎn)F到平面DCE的距離為![]() ,求直線EC與平面BDE所成角的正弦值.
,求直線EC與平面BDE所成角的正弦值.
【答案】(1)見解析;
(2)![]() .
.
【解析】
(1)由題意及勾股數(shù)可證得平面![]() 平面
平面![]() ,再由面面垂直的性質(zhì)可證DE與平面ABCD垂直,可得AC⊥DE,再結(jié)合菱形中的垂直證得
,再由面面垂直的性質(zhì)可證DE與平面ABCD垂直,可得AC⊥DE,再結(jié)合菱形中的垂直證得![]() 平面
平面![]() ,從而得到結(jié)論;
,從而得到結(jié)論;
(2)設(shè)![]() ,連接
,連接![]() .由(1)
.由(1)![]() 平面
平面![]() ,則
,則![]() 是
是![]() 在平面
在平面![]() 內(nèi)的射影,可得
內(nèi)的射影,可得![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .由點(diǎn)F到平面DCE的距離可得菱形
.由點(diǎn)F到平面DCE的距離可得菱形![]() 中,
中,![]() ,可求得OC,在
,可求得OC,在![]() 中,可求得EC,則可得結(jié)果.
中,可求得EC,則可得結(jié)果.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴AC⊥DE.①
∵四邊形![]() 為菱形,
為菱形,
∴![]() . ②
. ②
由①②,且![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() .
.
(2)設(shè)![]() ,連接
,連接![]() .
.
由(1)![]() 平面
平面![]() ,∴
,∴![]() 是
是![]() 在平面
在平面![]() 內(nèi)的射影,
內(nèi)的射影,
∴![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.

∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴點(diǎn)![]() 到平面
到平面![]() 的距離等于點(diǎn)
的距離等于點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
在平面![]() 內(nèi)作
內(nèi)作![]() ,交
,交![]() 延長線于
延長線于![]() .
.
∵平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .(或轉(zhuǎn)化為點(diǎn)
.(或轉(zhuǎn)化為點(diǎn)![]() 到平面
到平面![]() 的距離)
的距離)
∵![]() ,∴
,∴![]() ,
,
∴菱形![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某花店每天以每枝![]() 元的價(jià)格從農(nóng)場購進(jìn)若干枝玫瑰花,然后以每枝
元的價(jià)格從農(nóng)場購進(jìn)若干枝玫瑰花,然后以每枝![]() 元的價(jià)格出售,如果當(dāng)天賣不完,剩下的玫瑰花作垃圾處理.
元的價(jià)格出售,如果當(dāng)天賣不完,剩下的玫瑰花作垃圾處理.
(1)若花店一天購進(jìn)![]() 枝玫瑰花,求當(dāng)天的利潤
枝玫瑰花,求當(dāng)天的利潤![]() (單位:元)關(guān)于當(dāng)天需求量
(單位:元)關(guān)于當(dāng)天需求量![]() (單位:枝,
(單位:枝,![]() )的函數(shù)解析式.
)的函數(shù)解析式.
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
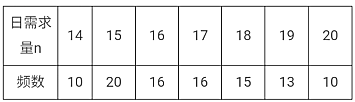
以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率.
(i)若花店一天購進(jìn)![]() 枝玫瑰花,
枝玫瑰花,![]() 表示當(dāng)天的利潤(單位:元),求
表示當(dāng)天的利潤(單位:元),求![]() 的分布列,數(shù)學(xué)期望及方差;
的分布列,數(shù)學(xué)期望及方差;
(ii)若花店計(jì)劃一天購進(jìn)16枝或17枝玫瑰花,你認(rèn)為應(yīng)購進(jìn)16枝還是17枝?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,若點(diǎn)
,若點(diǎn)![]() 是曲線
是曲線![]() 截直線
截直線![]() 所得線段的中點(diǎn),求
所得線段的中點(diǎn),求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種產(chǎn)品的質(zhì)量以其質(zhì)量指標(biāo)值衡量,并依據(jù)質(zhì)量指標(biāo)值劃分等級如表:
質(zhì)量指標(biāo)值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m≤65 |
等級 | 一等品 | 二等品 | 三等品 |
某企業(yè)從生產(chǎn)的這種產(chǎn)品中抽取100件產(chǎn)品作為樣本,檢測其質(zhì)量指標(biāo)值,得到如圖所示的頻率分布直方圖.(同一組數(shù)據(jù)用該區(qū)間的中點(diǎn)值作代表):
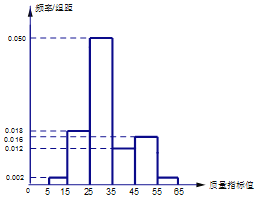
(1)根據(jù)以上抽樣調(diào)查數(shù)據(jù),能否認(rèn)為該企業(yè)生產(chǎn)的這種產(chǎn)品符合“一、二等品至少要占全部產(chǎn)品82%”的規(guī)定?
(2)該企業(yè)為提高產(chǎn)品質(zhì)量,開展了“質(zhì)量提升月”活動(dòng),活動(dòng)后再抽樣檢測,產(chǎn)品質(zhì)量指標(biāo)值X近似滿足X~N(31,122),則“質(zhì)量提升月”活動(dòng)后的質(zhì)量指標(biāo)值的均值比活動(dòng)前大約提升或降低多少?
(3)若企業(yè)每件一等品售價(jià)180元,每件二等品售價(jià)150元,每件三等品售價(jià)120元,以樣本中的頻率代替相應(yīng)概率,現(xiàn)有一名顧客隨機(jī)購買兩件產(chǎn)品,設(shè)其支付的費(fèi)用為X(單位:元),求X的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() ,
,![]() 是離心率為
是離心率為![]() 的橢圓的左、右頂點(diǎn),
的橢圓的左、右頂點(diǎn),![]() ,
,![]() 是該橢圓的左、右焦點(diǎn),
是該橢圓的左、右焦點(diǎn),![]() ,
,![]() 是直線
是直線![]() 上兩個(gè)動(dòng)點(diǎn),連接
上兩個(gè)動(dòng)點(diǎn),連接![]() 和
和![]() ,它們分別與橢圓交于點(diǎn)
,它們分別與橢圓交于點(diǎn)![]() ,
,![]() 兩點(diǎn),且線段
兩點(diǎn),且線段![]() 恰好過橢圓的左焦點(diǎn)
恰好過橢圓的左焦點(diǎn)![]() .當(dāng)
.當(dāng)![]() 時(shí),點(diǎn)
時(shí),點(diǎn)![]() 恰為線段
恰為線段![]() 的中點(diǎn).
的中點(diǎn).
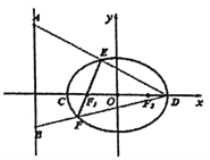
(1)求橢圓的方程;
(Ⅱ)判斷以![]() 為直徑的圓與直線
為直徑的圓與直線![]() 位置關(guān)系,并加以證明.
位置關(guān)系,并加以證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列有關(guān)命題的說法正確的是( )
A.命題“若![]() ⊥
⊥![]() ,則
,則![]()
![]() 0”的否命題為“若
0”的否命題為“若![]() ⊥
⊥![]() ,則
,則![]()
![]() 0”
0”
B.命題“函數(shù)f(x)=(a﹣1)x是R上的增函數(shù)”的否定是“函數(shù)f(x)=(a﹣1)x是R上的減函數(shù)”
C.命題“在△ABC中,若sinA=sinB,則A=B”的逆否命題為真命題
D.命題“若x=2,則x2﹣3x+2=0”的逆命題為真命題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面角坐標(biāo)系![]() 中,以坐標(biāo)原點(diǎn)
中,以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸的正半軸為極軸建立極坐標(biāo)系,已知曲線
軸的正半軸為極軸建立極坐標(biāo)系,已知曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,將曲線
,將曲線![]() 向左平移
向左平移![]() 個(gè)單位長度得到曲線
個(gè)單位長度得到曲線![]() .
.
(1)求曲線![]() 的參數(shù)方程;
的參數(shù)方程;
(2)已知![]() 為曲線
為曲線![]() 上的動(dòng)點(diǎn),
上的動(dòng)點(diǎn), ![]() 兩點(diǎn)的極坐標(biāo)分別為
兩點(diǎn)的極坐標(biāo)分別為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國倉儲指數(shù)是反映倉儲行業(yè)經(jīng)營和國內(nèi)市場主要商品供求狀況與變化趨勢的已套指數(shù)體系.如圖所示的折線圖是2017年和2018年的中國倉儲指數(shù)走勢情況.根據(jù)該折線圖,下列結(jié)論中不正確的是( )
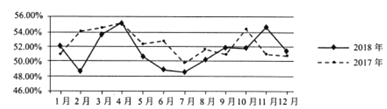
A. 2018年1月至4月的倉儲指數(shù)比2017年同期波動(dòng)性更大
B. 這兩年的最大倉儲指數(shù)都出現(xiàn)在4月份
C. 2018年全年倉儲指數(shù)平均值明顯低于2017年
D. 2018年各倉儲指數(shù)的中位數(shù)與2017年各倉儲指數(shù)中位數(shù)差異明顯
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若一個(gè)四位數(shù)的各位數(shù)字相加和為10,則稱該數(shù)為“完美四位數(shù)”,如數(shù)字“2017”.試問用數(shù)字0,1,2,3,4,5,6,7組成的無重復(fù)數(shù)字且大于2017的“完美四位數(shù)”有( )個(gè).
A. 71B. 66C. 59D. 53
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com