
【題目】已知四棱錐P-ABCD中,底面ABCD為直角梯形,![]() 平面ABCD,且
平面ABCD,且![]()
![]()
![]()
![]() .
.
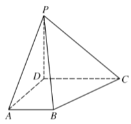
(1)求證:![]() 平面PBD;
平面PBD;
(2)若PB與平面ABCD所成的角為![]() ,求二面角D-PC-B的余弦值.
,求二面角D-PC-B的余弦值.
【答案】(1)證明見解析,(2)![]()
【解析】
(1)取CD的中點E,連接AE,BE,BD,證明四邊形ABED為正方形,得到![]() ,再由線面垂直可得
,再由線面垂直可得![]() ,即可證明
,即可證明![]() 平面PBD,再證四邊形ABCE為平行四邊形,即可得證.
平面PBD,再證四邊形ABCE為平行四邊形,即可得證.
(2)以點D為坐標原點,分別以DA,DC,DP所在直線為x,y,z軸,建立空間直角坐標系,利用空間向量法求出二面角的余弦值.
解:(1)證明:取CD的中點E,連接AE,BE,BD.
![]()
![]() .
.
又![]()
![]() ,
,
![]() 四邊形ABED為正方形,則
四邊形ABED為正方形,則![]() .
.
![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
![]() .
.
![]()
![]() 平面PBD,
平面PBD,![]() 平面PBD.
平面PBD.
![]() 平面PBD.
平面PBD.
![]()
![]() ,
,
![]() 四邊形ABCE為平行四邊形,
四邊形ABCE為平行四邊形,
![]()
![]() 平面PBD.
平面PBD.
(2)![]() 平面ABCD,
平面ABCD,
![]() 為PB與平面ABCD所成的角,
為PB與平面ABCD所成的角,
即![]() ,則
,則![]() .
.
設![]() ,則
,則![]()
![]()
![]() .
.
以點D為坐標原點,分別以DA,DC,DP所在直線為x,y,z軸,建立如圖所示的空間直角坐標系,
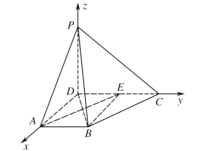
則![]()
![]()
![]()
![]() ,
,![]() .
.
![]()
![]() 平面PDC,
平面PDC,
![]() 平面PDC的一個法向量
平面PDC的一個法向量![]() .
.
設平面PBC的法向量![]() ,
,
![]()
![]() ,
,
則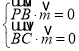
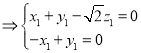 ,
,
取![]() ,則
,則![]() .
.
設二面角D-PC-B的平面角為![]() ,
,
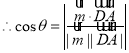
![]()
![]() .
.
由圖可知二面角D-PC-B為銳角,
故二面角D-PC-B的余弦值為![]() .
.


科目:高中數學 來源: 題型:
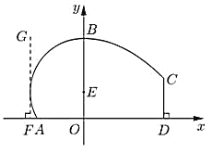
【題目】某地擬建造一座體育館,其設計方案側面的外輪廓線如圖所示:曲線![]() 是以點
是以點![]() 為圓心的圓的一部分,其中
為圓心的圓的一部分,其中![]()
![]() ,
,![]() 是圓的切線,且
是圓的切線,且![]() ,曲線
,曲線![]() 是拋物線
是拋物線![]()
![]() 的一部分,
的一部分,![]() ,且
,且![]() 恰好等于圓
恰好等于圓![]() 的半徑.
的半徑.
(1)若![]() 米,
米,![]() 米,求
米,求![]() 與
與![]() 的值;
的值;
(2)若體育館側面的最大寬度![]() 不超過75米,求
不超過75米,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公比大于
是公比大于![]() 的等比數列,
的等比數列,![]() 為數列
為數列![]() 的前
的前![]() 項和,
項和,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差數列.數列
成等差數列.數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() 滿足
滿足![]() ,且
,且![]() ,
,
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)令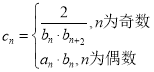 ,求數列
,求數列![]() 的前
的前![]() 項和為
項和為![]() ;
;
(3)將數列![]() ,
,![]() 的項按照“當
的項按照“當![]() 為奇數時,
為奇數時,![]() 放在前面;當
放在前面;當![]() 為偶數時,
為偶數時,![]() 放在前面”的要求進行排列,得到一個新的數列:
放在前面”的要求進行排列,得到一個新的數列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求這個新數列的前
,求這個新數列的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 為兩非零有理數列(即對任意的
為兩非零有理數列(即對任意的![]() ,
,![]() ,
,![]() 均為有理數),
均為有理數),![]() 為一個無理數列(即對任意的
為一個無理數列(即對任意的![]() ,
,![]() 為無理數).
為無理數).
(1)已知![]() ,并且
,并且![]() 對任意的
對任意的![]() 恒成立,試求
恒成立,試求![]() 的通項公式;
的通項公式;
(2)若![]() 為有理數列,試證明:對任意的
為有理數列,試證明:對任意的![]() ,
,![]() 恒成立的充要條件為
恒成立的充要條件為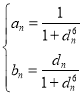 ;
;
(3)已知![]() ,
,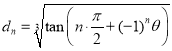 ,試計算
,試計算![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(I)試判斷函數![]() 的單調性;
的單調性;
(Ⅱ)若函數![]()
![]() 在
在![]() 上有且僅有一個零點,
上有且僅有一個零點,
(i)求證:此零點是![]() 的極值點;
的極值點;
(ⅱ)求證:![]() .
.
(本題可能會用到的數據:![]()
![]()
![]()
![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的十九大報告指出,在全面建成小康社會的決勝階段,讓貧困地區同全國人民共同進入全面小康社會是我們黨的莊嚴承諾.在“脫真貧、真脫貧”的過程中,精準扶貧助推社會公平顯得尤其重要.若某地區有100戶貧困戶,經過一年扶貧后,為了考查該地區的“精準扶貧”的成效![]() 該地區脫貧標準為“每戶人均年收入不少于4000元”
該地區脫貧標準為“每戶人均年收入不少于4000元”![]() ,現從該地區隨機抽取A、B兩個村莊,再從這兩個村莊的貧困戶中隨機抽取20戶,調查每戶的現人均年收入,繪制如圖所示的莖葉圖
,現從該地區隨機抽取A、B兩個村莊,再從這兩個村莊的貧困戶中隨機抽取20戶,調查每戶的現人均年收入,繪制如圖所示的莖葉圖![]() 單位:百元
單位:百元![]() .
.
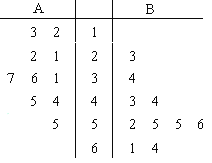
(1)觀察莖葉圖中的數據,判斷哪個村莊扶貧成效較好?并說明理由;
(2)計劃對沒有脫貧的貧困戶進一步實行“精準扶貧”,下一年的資金投入方案如下:對人均年收入不高于2000元的貧困戶,每戶每年增加扶貧資金5000元;對人均年收入高于2000元但不高于3000元的貧困戶,每戶每年增加扶貧資金3000元;對人均年收入高于3000元但不高于4000元的貧困戶,每戶每年增加扶貧資金1000元;對已經脫貧的貧困戶不再增加扶貧資金投入.依據此方案,試估計下一年該地區共需要增加扶貧資金多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(a,b∈R)為奇函數.
,(a,b∈R)為奇函數.
(1)求b值;
(2)當a=﹣2時,存在x0∈[1,4]使得不等式f(x0)≤t成立,求實數t的取值范圍;
(3)當a≥1時,求證:函數g(x)=f(2x)﹣c(c∈R)在區間(﹣∞,﹣1]上至多有一個零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的所有項都是不等于
的所有項都是不等于![]() 的正數,
的正數,![]() 的前
的前![]() 項和為
項和為![]() ,已知點
,已知點![]() 在直線
在直線![]() 上(其中常數
上(其中常數![]() ,且
,且![]() )數列,又
)數列,又![]() .
.
(1)求證數列![]() 是等比數列;
是等比數列;
(2)如果![]() ,求實數
,求實數![]() 的值;
的值;
(3)若果存在![]() 使得點
使得點![]() 和
和![]() 都在直線在
都在直線在![]() 上,是否存在自然數
上,是否存在自然數![]() ,當
,當![]() (
(![]() )時,
)時,![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com