【題目】某同學為研究“網絡游戲對當代青少年的影響”作了一次調查，共調查了50名同學，其中男生26人，有8人不喜歡玩游戲，而調查的女生中有9人喜歡玩游戲.
（1）根據以上數據完成2×2的列聯表；
（2）根據以上數據，在犯錯誤的概率不超過0.025的前提下，能否認為“喜歡玩電腦游戲與性別有關系”？
男生 | 女生 | 總計 | |
喜歡玩游戲 | |||
不喜歡玩游戲 | |||
總計 |
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
舉一反三期末百分沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】下列事件：①任取這三條線段，這三條線段恰好組成直角三角形；②從一個三角形的三個頂點各任畫一條射線，這三條射線交于一點；③實數
，
都不為，但
；④明年12月28日的最高氣溫高于今年12月28日的最高氣溫.其中為隨機事件的是（ ）
A.①②③④B.①②④C.①③④D.②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
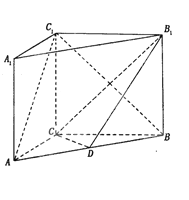
【題目】如圖所示, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AB=5，AA1＝4，點D是AB的中點，
（1）求證： AC1//平面CDB1；
（2）求二面角C1-AB-C的平面角的正切值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據調查，某學校開設了“街舞”、“圍棋”、“武術”三個社團，三個社團參加的人數如下表所示：
社團 | 街舞 | 圍棋 | 武術 |
人數 | 320 | 240 | 200 |
為調查社團開展情況，學校社團管理部采用分層抽樣的方法從中抽取一個容量為n的樣本，已知從“圍棋”社團抽取的同學比從“街舞”社團抽取的同學少2人.
（1）求三個社團分別抽取了多少同學；
（2）若從“圍棋”社團抽取的同學中選出2人擔任該社團活動監督的職務，已知“圍棋”社團被抽取的同學中有2名女生，求至少有1名女同學被選為監督職務的概率。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校有n個班（n為給定正整數），且每班的男生與女生人數至多相差1．現該學校進行乒乓球比賽，規則如下：同一班的選手之間不比賽，不同班的每兩名選手都比賽一場．我們稱在同性別選手間的比賽為同打，異性別選手間的比賽為異打．若同打場數與異打場數至多相差1，求有奇數名學生的班級至多有多少個？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】心理學家分析發現視覺和空間能力與性別有關，某數學興趣小組為了驗證這個結論，從興趣小組中按分層抽樣的方法抽取
名同學（男
女
），給所有同學幾何題和代數題各一題，讓各位同學自由選擇一道題進行解答.選題情況如下表：（單位：人）
幾何題 | 代數題 | 總計 | |
男同學 |
|
|
|
女同學 |
|
|
|
總計 |
|
|
|
（1）能否據此判斷有
的把握認為視覺和空間能力與性別有關？
（2）經過多次測試后，甲每次解答一道幾何題所用的時間在
分鐘，乙每次解答一道幾何題所用的時間在
分鐘，現甲、乙各解同一道幾何題，求乙比甲先解答完的概率.
（3）現從選擇做幾何的
名女生中任意抽取兩人對她們的答題情況進行全程研究，記甲、乙兩女生被抽到的人數為
，求的分布列及數學期望
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的方程為
，點
為坐標原點，點
，
的坐標分別為
，
，
，直線
的斜率為
.
（1）求橢圓的方程；
（2）若斜率為
的直線
交橢圓于
，
兩點，交
軸于點
，問是否存在實數
使得以
為直徑的圓恒過點？若存在，求的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知正方體ABCD－A1B1C1D1的棱長為1，E，F分別是棱AD，B1C1上的動點，設AE＝λ，B1F＝μ．若平面BEF與正方體的截面是五邊形，則λ＋μ的取值范圍是________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
