
【題目】已知橢圓![]() 的離心率
的離心率![]() ,其左、右頂點(diǎn)分別為點(diǎn)
,其左、右頂點(diǎn)分別為點(diǎn)![]() ,且點(diǎn)
,且點(diǎn)![]() 關(guān)于直線
關(guān)于直線![]() 對(duì)稱的點(diǎn)在直線
對(duì)稱的點(diǎn)在直線![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若點(diǎn)![]() 在橢圓
在橢圓![]() 上,點(diǎn)
上,點(diǎn)![]() 在圓
在圓![]() 上,且
上,且![]() 都在第一象限,
都在第一象限,![]() 軸,若直線
軸,若直線![]() 與
與![]() 軸的交點(diǎn)分別為
軸的交點(diǎn)分別為![]() ,判斷
,判斷![]() 是否為定值,若是定值,求出該定值;若不是定值,說明理由.
是否為定值,若是定值,求出該定值;若不是定值,說明理由.
【答案】(1)![]() ;(2)1.
;(2)1.
【解析】
(1)點(diǎn)![]() 關(guān)于直線
關(guān)于直線![]() 對(duì)稱的點(diǎn)
對(duì)稱的點(diǎn)![]() 在直線
在直線![]() 上,代入可求出
上,代入可求出![]() ,又
,又![]() ,可解出
,可解出![]() ,然后得出橢圓方程;(2)設(shè)
,然后得出橢圓方程;(2)設(shè)![]() ,
,![]() ,求出點(diǎn)
,求出點(diǎn)![]() 的坐標(biāo),聯(lián)立直線與橢圓方程,由韋達(dá)定理求出
的坐標(biāo),聯(lián)立直線與橢圓方程,由韋達(dá)定理求出![]() 坐標(biāo),從而得到
坐標(biāo),從而得到![]() 的方程,求出點(diǎn)
的方程,求出點(diǎn)![]() 的坐標(biāo),設(shè)
的坐標(biāo),設(shè)![]() ,求出
,求出![]() 化簡(jiǎn)得
化簡(jiǎn)得![]() ,所以
,所以![]() ,
,![]() 為定值.
為定值.
解:(1)點(diǎn)![]() 關(guān)于直線
關(guān)于直線![]() 對(duì)稱的點(diǎn)
對(duì)稱的點(diǎn)![]() 在直線
在直線![]() 上,
上,
∴![]() ,解得
,解得![]() .
.
又![]() ,解得
,解得![]() .
.
∴橢圓E的方程為:![]() .
.
(2)設(shè)![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,∴
,∴![]() .
.
聯(lián)立![]() ,化簡(jiǎn)得:
,化簡(jiǎn)得:![]() .
.
∴![]() ,解得
,解得![]() .
.
∴![]() ,即
,即![]() .
.
∴直線![]() 的斜率=
的斜率=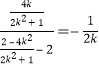 .
.
∴![]() 的方程:
的方程:![]() ,令
,令![]() ,解得
,解得![]() ,∴
,∴![]() .
.
設(shè)![]() ,則
,則![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() 為定值.
為定值.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從某公司生產(chǎn)線生產(chǎn)的某種產(chǎn)品中抽取![]() 件,測(cè)量這些產(chǎn)品的一項(xiàng)質(zhì)量指標(biāo),由檢測(cè)結(jié)果得如圖所示的頻率分布直方圖:
件,測(cè)量這些產(chǎn)品的一項(xiàng)質(zhì)量指標(biāo),由檢測(cè)結(jié)果得如圖所示的頻率分布直方圖:
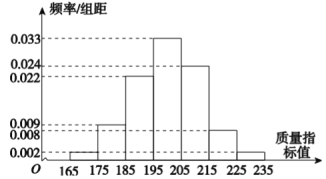
(Ⅰ)求這![]() 件產(chǎn)品質(zhì)量指標(biāo)的樣本平均數(shù)
件產(chǎn)品質(zhì)量指標(biāo)的樣本平均數(shù)![]() 和樣本方差
和樣本方差![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作代表);
(Ⅱ)由直方圖可以認(rèn)為,這種產(chǎn)品的質(zhì)量指標(biāo)值![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,其中
,其中![]() 近似為樣本平均數(shù)
近似為樣本平均數(shù)![]() 近似為樣本方差
近似為樣本方差![]() .
.
(i)利用該正態(tài)分布,求![]() ;
;
(ii)已知每件該產(chǎn)品的生產(chǎn)成本為![]() 元,每件合格品(質(zhì)量指標(biāo)值
元,每件合格品(質(zhì)量指標(biāo)值![]() )的定價(jià)為
)的定價(jià)為![]() 元;若為次品(質(zhì)量指標(biāo)值
元;若為次品(質(zhì)量指標(biāo)值![]() ),除了全額退款外且每件次品還須賠付客戶
),除了全額退款外且每件次品還須賠付客戶![]() 元。若該公司賣出
元。若該公司賣出![]() 件這種產(chǎn)品,記
件這種產(chǎn)品,記![]() 表示這件產(chǎn)品的利潤(rùn),求
表示這件產(chǎn)品的利潤(rùn),求![]() .
.
附:![]() .若
.若![]() ,則
,則![]()
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M為線段AD上一點(diǎn),AM=2MD,N為PC的中點(diǎn).

(Ⅰ)證明MN∥平面PAB;
(Ⅱ)求直線AN與平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市為了解社區(qū)群眾體育活動(dòng)的開展情況,擬采用分層抽樣的方法從A,B,C三個(gè)行政區(qū)抽出6個(gè)社區(qū)進(jìn)行調(diào)查.已知A,B,C行政區(qū)中分別有12,18,6個(gè)社區(qū).
(1)求從A,B,C三個(gè)行政區(qū)中分別抽取的社區(qū)個(gè)數(shù);
(2)若從抽得的6個(gè)社區(qū)中隨機(jī)的抽取2個(gè)進(jìn)行調(diào)查結(jié)果的對(duì)比,求抽取的2個(gè)社區(qū)中至少有一個(gè)來自A行政區(qū)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知從1開始的連續(xù)奇數(shù)蛇形排列形成寶塔形數(shù)表,第一行為1,第二行為3,5,第三行為7,9,11,第四行為13,15,17,19,如圖所示,在寶塔形數(shù)表中位于第![]() 行,第
行,第![]() 列的數(shù)記為
列的數(shù)記為![]() ,比如
,比如![]() ,
,![]() ,
,![]() ,若
,若![]() ,則
,則![]() ( )
( )

A. 72B. 71C. 66D. 65
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為評(píng)估設(shè)備![]() 生產(chǎn)某種零件的性能,從設(shè)備
生產(chǎn)某種零件的性能,從設(shè)備![]() 生產(chǎn)零件的流水線上隨機(jī)抽取100件零件作為樣本,測(cè)量其直徑后,整理得到下表:
生產(chǎn)零件的流水線上隨機(jī)抽取100件零件作為樣本,測(cè)量其直徑后,整理得到下表:
直徑 | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計(jì) |
件數(shù) | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經(jīng)計(jì)算,樣本的平均值![]() ,標(biāo)準(zhǔn)差
,標(biāo)準(zhǔn)差![]() ,以頻率值作為概率的估計(jì)值,用樣本估計(jì)總體.
,以頻率值作為概率的估計(jì)值,用樣本估計(jì)總體.
(1)將直徑小于等于![]() 或直徑大于
或直徑大于![]() 的零件認(rèn)為是次品,從設(shè)備
的零件認(rèn)為是次品,從設(shè)備![]() 的生產(chǎn)流水線上隨意抽取3個(gè)零件,計(jì)算其中次品個(gè)數(shù)
的生產(chǎn)流水線上隨意抽取3個(gè)零件,計(jì)算其中次品個(gè)數(shù)![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望![]() ;
;
(2)為評(píng)判一臺(tái)設(shè)備的性能,從該設(shè)備加工的零件中任意抽取一件,記其直徑為![]() ,并根據(jù)以下不等式進(jìn)行評(píng)判(
,并根據(jù)以下不等式進(jìn)行評(píng)判(![]() 表示相應(yīng)事件的概率):①
表示相應(yīng)事件的概率):①![]() ;②
;②![]() ;③
;③![]() .評(píng)判規(guī)則為:若同時(shí)滿足上述三個(gè)不等式,則設(shè)備等級(jí)為甲;僅滿足其中兩個(gè),則等級(jí)為乙;若僅滿足其中一個(gè),則等級(jí)為丙;若全部不滿足,則等級(jí)為丁,試判斷設(shè)備
.評(píng)判規(guī)則為:若同時(shí)滿足上述三個(gè)不等式,則設(shè)備等級(jí)為甲;僅滿足其中兩個(gè),則等級(jí)為乙;若僅滿足其中一個(gè),則等級(jí)為丙;若全部不滿足,則等級(jí)為丁,試判斷設(shè)備![]() 的性能等級(jí)并說明理由.
的性能等級(jí)并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知過定點(diǎn)![]() 的動(dòng)圓是
的動(dòng)圓是![]() 與圓
與圓![]() 相內(nèi)切.
相內(nèi)切.
(1)求動(dòng)圓圓心![]() 的軌跡方程;
的軌跡方程;
(2)設(shè)動(dòng)圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,
,![]() 是曲線
是曲線![]() 上的兩點(diǎn),線段
上的兩點(diǎn),線段![]() 的垂直平分線過點(diǎn)
的垂直平分線過點(diǎn)![]() ,求
,求![]() 面積的最大值(
面積的最大值(![]() 是坐標(biāo)原點(diǎn)).
是坐標(biāo)原點(diǎn)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,已知拋物線C:![]() 的焦點(diǎn)為F,過F的直線
的焦點(diǎn)為F,過F的直線![]() 交拋物線C于A,B兩點(diǎn).
交拋物線C于A,B兩點(diǎn).
(1)求線段AF的中點(diǎn)M的軌跡方程;
(2)已知△AOB的面積是△BOF面積的3倍,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是邊長(zhǎng)為2的菱形,且
是邊長(zhǎng)為2的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是線段
是線段![]() 上任意一點(diǎn).
上任意一點(diǎn).
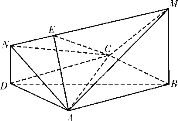
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 的最大值是
的最大值是![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com