
已知等差數(shù)列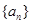 的前
的前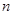 項和為
項和為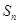 ,公差
,公差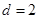 ,且
,且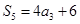 .
.
(1)求數(shù)列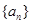 的通項公式;
的通項公式;
(2)設(shè)數(shù)列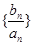 是首項為1,公比為
是首項為1,公比為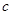 的等比數(shù)列,求數(shù)列
的等比數(shù)列,求數(shù)列 的前n項和
的前n項和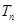 .
.
(1)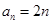 (2)
(2) 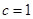 時,
時,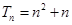 ;
;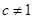 時,
時,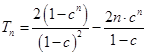
解析試題分析:(1)將已知條件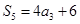 中的
中的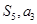 均用
均用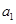 表示,即可解得
表示,即可解得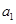 的值。再根據(jù)等差的通項公式求其通項公式即可。(2)根據(jù)等比數(shù)列的通項公式可得
的值。再根據(jù)等差的通項公式求其通項公式即可。(2)根據(jù)等比數(shù)列的通項公式可得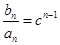 ,即可得
,即可得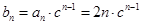 (注意對公比
(注意對公比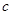 是否為1進行討論)。當(dāng)
是否為1進行討論)。當(dāng)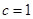 時,
時,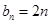 ,根據(jù)等差數(shù)列前
,根據(jù)等差數(shù)列前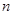 項和公式求
項和公式求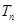 ;當(dāng)
;當(dāng)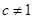 時,
時,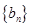 的通項公式等于等差乘等比的形式,故應(yīng)用錯位相減法求其前n項和
的通項公式等于等差乘等比的形式,故應(yīng)用錯位相減法求其前n項和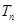 。
。
解:(1)因為公差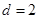 ,且
,且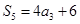 ,
,
所以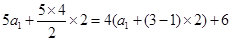 . 2分
. 2分
所以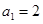 . 4分
. 4分
所以等差數(shù)列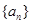 的通項公式為
的通項公式為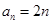 . 5分
. 5分
(2)因為數(shù)列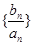 是首項為1,公比為
是首項為1,公比為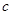 的等比數(shù)列,
的等比數(shù)列,
所以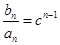 . 6分
. 6分
所以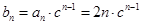 . 7分
. 7分
(1)當(dāng)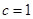 時,
時,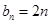 . 8分
. 8分
所以 . 9分
. 9分
(2)當(dāng)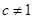 時,
時,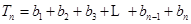
因為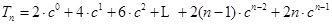 ① 9分
① 9分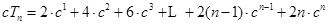 ② 10分
② 10分
①-②得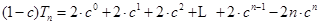 11分
11分
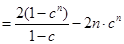 12分
12分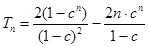 13分
13分
考點:1等差數(shù)列的通項公式、前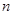 項和公式;2錯位相減法求數(shù)列前
項和公式;2錯位相減法求數(shù)列前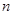 項和。
項和。


 通城學(xué)典默寫能手系列答案
通城學(xué)典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
在數(shù)列{an}中,an+1+an=2n-44(n∈N*),a1=-23.
(1)求an;
(2)設(shè)Sn為{an}的前n項和,求Sn的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(2012•廣東)設(shè)數(shù)列{an}的前n項和為Sn,滿足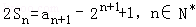 ,且a1,a2+5,a3成等差數(shù)列.
,且a1,a2+5,a3成等差數(shù)列.
(1)求a1的值;
(2)求數(shù)列{an}的通項公式;
(3)證明:對一切正整數(shù)n,有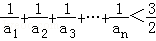 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(2013·安徽高考)設(shè)數(shù)列{an}滿足a1=2,a2+a4=8,且對任意n∈N*,函數(shù)f(x)=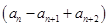 x+an+1cos x-an+2sin x滿足f′
x+an+1cos x-an+2sin x滿足f′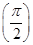 =0.
=0.
(1)求數(shù)列{an}的通項公式;
(2)若bn=2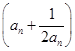 ,求數(shù)列{bn}的前n項和Sn.
,求數(shù)列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(2013•浙江)在公差為d的等差數(shù)列{an}中,已知a1=10,且a1,2a2+2,5a3成等比數(shù)列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
拋物線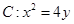 ,直線
,直線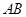 過拋物線
過拋物線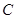 的焦點
的焦點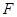 ,交
,交 軸于點
軸于點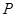 .
.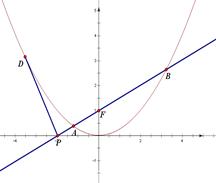
(1)求證: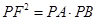 ;
;
(2)過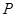 作拋物線
作拋物線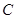 的切線,切點為
的切線,切點為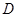 (異于原點),
(異于原點),
(ⅰ)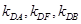 是否恒成等差數(shù)列,請說明理由;
是否恒成等差數(shù)列,請說明理由;
(ⅱ)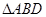 重心的軌跡是什么圖形,請說明理由.
重心的軌跡是什么圖形,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
下列命題正確的是 ( )
①若數(shù)列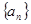 是等差數(shù)列,且
是等差數(shù)列,且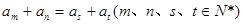 ,
,
則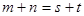 ;
;
②若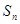 是等差數(shù)列
是等差數(shù)列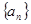 的前
的前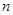 項的和,則
項的和,則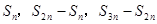 成等差數(shù)列;
成等差數(shù)列;
③若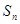 是等比數(shù)列
是等比數(shù)列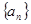 的前
的前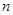 項的和,則
項的和,則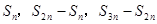 成等比數(shù)列;
成等比數(shù)列;
④若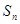 是等比數(shù)列
是等比數(shù)列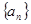 的前
的前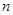 項的和,且
項的和,且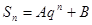 ;(其中
;(其中 是非零常數(shù),
是非零常數(shù),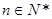 ),則
),則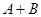 為零.
為零.
| A.①② | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知公差不為零的等差數(shù)列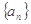 ,等比數(shù)列
,等比數(shù)列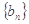 ,滿足
,滿足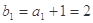 ,
,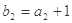 ,
,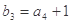 .
.
(1)求數(shù)列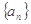 、
、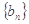 的通項公式;
的通項公式;
(2)若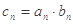 ,求數(shù)列{
,求數(shù)列{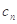 }的前n項和.
}的前n項和.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com