【題目】設f(a)＝|x2－a2|dx
（1）當0≤a≤1與a＞1時，分別求f(a)；
（2）當a≥0時，求f(a)的最小值．
【答案】
（1）
【解答】
當0≤a≤1時，
當a>1時，
所以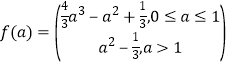
（2）
【解答】
當a>1時，由于
在
上是增函數，
故f(a)在上的最小值是
,
當
時，f'(a)=4a2-2a=2a(2a-1),
由f(a)>0知，
或a<0,
故f(a)在
上遞減 ，在
上遞增，
因此在[0,1]上，f(a)的最小值為
,
綜上可知，f(a)在
上的最小值為
.
【解析】因為f(a)＝|x2－a2|dx中帶有絕對值，在計算的過程中首先要分類討論去掉絕對值，本題考查了分類討論求解問題的能力，難度較大
【考點精析】解答此題的關鍵在于理解定積分的概念的相關知識，掌握定積分的值是一個常數，可正、可負、可為零；用定義求定積分的四個基本步驟：①分割；②近似代替；③求和；④取極限．
科目：高中數學 來源： 題型：
【題目】已知直線l：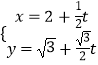 
（t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C的極坐標方程為ρ=2．
（1）若點M的直角坐標為（2， 
），直線l與曲線C交于A、B兩點，求|MA|+|MB|的值；
（2）設曲線C經過伸縮變換 
得到曲線C′，求曲線C′的內接矩形周長的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在三棱錐S﹣ABC中，△ABC是邊長為2 
的正三角形，平面SAC⊥平面ABC，SA=SC=2，M、N分別為AB、SB的中點．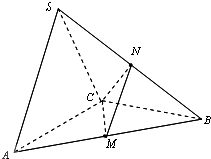 
（1）證明：AC⊥SB；
（2）求三棱錐B﹣CMN的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2x+2﹣x ． （Ⅰ）試寫出這個函數的性質（不少于3條，不必說明理由），并作出圖象；
（Ⅱ）設函數g（x）=4x+4﹣x﹣af（x），求這個函數的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，其中 n 為正整數．
（1）求f(1),f(2),f(3) 的值；
（2）猜想滿足不等式 f(n)<0 的正整數 n 的范圍，并用數學歸納法證明你的猜想．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用數學歸納法證明
，則當n=k+1時左端應在n=k的基礎上加上（ ）
A.（3k+2）
B.（3k+4）
C.（3k+2）+（3k+3）
D.（3k+2）+（3k+3）+（3k+4）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
