
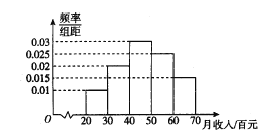
【題目】為了調查公司員工的飲食習慣與月收入之間的關系,隨機抽取了30名員工,并制作了這30人的月平均收入的頻率分布直方圖和飲食指數表(說明:圖中飲食指數低于70的人,飲食以蔬菜為主;飲食指數高于70的人,飲食以肉類為主).其中月收入4000元以上員工中有11人飲食指數高于70.
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
(1)是否有![]() 的把握認為飲食習慣與月收入有關系?若有,請說明理由,若沒有,說明理由并分析原因;
的把握認為飲食習慣與月收入有關系?若有,請說明理由,若沒有,說明理由并分析原因;
(2)從飲食指數在![]() 內的員工中任選2人,求他們的飲食指數均在
內的員工中任選2人,求他們的飲食指數均在![]() 內的概率;
內的概率;
(3)經調查某地若干戶家庭的年收入![]() (萬元)和年飲支出
(萬元)和年飲支出![]() (萬元)具有線性相關關系,并得到
(萬元)具有線性相關關系,并得到![]() 關于
關于![]() 的回歸直線方程:
的回歸直線方程:![]() .若一個員工的月收入恰好為這30人的月平均收入,估計該人的年飲食支出費用.
.若一個員工的月收入恰好為這30人的月平均收入,估計該人的年飲食支出費用.
附: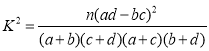 ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)有;(2)![]() ;(3)1.6881萬元.
;(3)1.6881萬元.
【解析】
(1)計算![]() ,根據
,根據![]() 值作出結論;(2)列出所有可能共10種,其中飲食指數均在
值作出結論;(2)列出所有可能共10種,其中飲食指數均在![]() 內的有3種,由古典概型求解即可(3)根據頻率分布直方圖求出此人月均收入,計算出年均收入代入回歸直線方程即可求解.
內的有3種,由古典概型求解即可(3)根據頻率分布直方圖求出此人月均收入,計算出年均收入代入回歸直線方程即可求解.
(1)根據頻率分布直方圖,月收入4000元以上的人數為![]() ,
,
所以完成下列![]() 列聯表如下:
列聯表如下:
月收入4000元以下 | 月收入4000元以上 | 合計 | |
主食 蔬菜 | 8 | 10 | 18 |
主食 肉類 | 1 | 11 | 12 |
合計 | 9 | 21 | 30 |
所以![]() ,故有
,故有![]() 的把握認為飲食習慣與月收入有關系,
的把握認為飲食習慣與月收入有關系,
(2)飲食指數在![]() 內的員工有5人,其中在
內的員工有5人,其中在![]() 的有3人,設為
的有3人,設為![]() ,在
,在![]() 的有2人,設為
的有2人,設為![]() ,從飲食指數在
,從飲食指數在![]() 內的員工中任選2人,
內的員工中任選2人,
所有結果為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10種,
,共10種,
其中他們的飲食指數均在![]() 內的結果為
內的結果為![]() ,
,![]() ,
,![]() ,共3種,
,共3種,
所以概率為![]() .
.
(3)根據頻率分布直方圖,![]() (百元),
(百元),
所以![]() (萬元),
(萬元),
故該人的年飲食支出費用約為1.6881萬元.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:高中數學 來源: 題型:
【題目】某蛋糕店每天制作生日蛋糕若干個,每個生日蛋糕成本為50元,每個蛋糕的售價為100元,如果當天賣不完,剩余的蛋糕作垃圾處理.現搜集并整理了100天生日蛋糕的日需求量(單位:個),得到如圖所示的柱狀圖.100天記錄的各需求量的頻率作為每天各需求量發生的概率.

(1)若該蛋糕店某一天制作生日蛋糕17個,設當天的需求量為![]() ,則當天的利潤
,則當天的利潤![]() (單位:元)是多少?
(單位:元)是多少?
(2)若蛋糕店一天制作17個生日蛋糕.
①求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() 的函數解析式;
的函數解析式;
②求當天的利潤不低于600圓的概率.
(3)若蛋糕店計劃一天制作16個或17個生日蛋糕,請你以蛋糕店一天利潤的平均值作為決策依據,應該制作16個還是17個生日蛋糕?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保障全國第四次經濟普查順利進行,國家統計局從東部選擇江蘇,從中部選擇河北、湖北,從西部選擇寧夏,從直轄市中選擇重慶作為國家綜合試點地區,然后再逐級確定普查區域,直到基層的普查小區,在普查過程中首先要進行宣傳培訓,然后確定對象,最后入戶登記,由于種種情況可能會導致入戶登記不夠順利,這為正式普查提供了寶貴的試點經驗,在某普查小區,共有50家企事業單位,150家個體經營戶,普查情況如下表所示:
普查對象類別 | 順利 | 不順利 | 合計 |
企事業單位 | 40 | 10 | 50 |
個體經營戶 | 100 | 50 | 150 |
合計 | 140 | 60 | 200 |
(1)寫出選擇5個國家綜合試點地區采用的抽樣方法;
(2)根據列聯表判斷是否有![]() 的把握認為“此普查小區的入戶登記是否順利與普查對象的類別有關”;
的把握認為“此普查小區的入戶登記是否順利與普查對象的類別有關”;
(3)以該小區的個體經營戶為樣本,頻率作為概率,從全國個體經營戶中隨機選擇3家作為普查對象,入戶登記順利的對象數記為![]() ,寫出
,寫出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地有A,B、C、D四人先后感染了新型冠狀病毒,其中只有A到過疫區,B肯定是受A感染的,對于C,因為難以判定他是受A還是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同樣也假設D受A、B和C感染的概率都是
,同樣也假設D受A、B和C感染的概率都是![]() .在這種假定之下,B、C、D中直接受A感染的人數X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數學期望)為______.
.在這種假定之下,B、C、D中直接受A感染的人數X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數學期望)為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點為別為
的左、右焦點為別為![]() 、
、![]() ,且過點
,且過點![]() 和
和![]() .
.
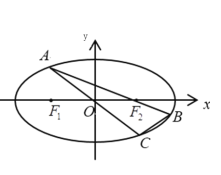
(1)求橢圓的標準方程;
(2)如圖,點![]() 為橢圓上一動點(非長軸端點),
為橢圓上一動點(非長軸端點),![]() 的延長線與橢圓交于點
的延長線與橢圓交于點![]() ,
,![]() 的延長線與橢圓交于點
的延長線與橢圓交于點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種賭博每局的規則是:賭客先在標記有1,2,3,4,5的卡片中隨機摸取一張,將卡片上的數字作為其賭金;隨后放回該卡片,再隨機摸取兩張,將這兩張卡片上數字之差的絕對值的1.4倍作為其獎金.若隨機變量ξ1和ξ2分別表示賭客在一局賭博中的賭金和獎金,則D(ξ1)=_____,E(ξ1)﹣E(ξ2)=_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學名著,書中把三角形的田稱為“圭田”,把直角梯形的田稱為“邪田”,稱底是“廣”,稱高是“正從”,“步”是丈量土地的單位.現有一邪田,廣分別為十步和二十步,正從為十步,其內有一塊廣為八步,正從為五步的圭田.若在邪田內隨機種植一株茶樹,求該株茶樹恰好種在圭田內的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,其中
,其中![]() .
.
(1)若![]() 滿足
滿足![]() .
.
①當![]() ,且
,且![]() 時,求
時,求![]() 的值;
的值;
②若存在互不相等的正整數![]() ,滿足
,滿足![]() ,且
,且![]() 成等差數列,求
成等差數列,求![]() 的值.
的值.
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com