
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以原點
為參數).在以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:解法一:(1)消去參數可得![]() 的普通方程為
的普通方程為![]() ,則極坐標方程為
,則極坐標方程為![]() .極坐標方程化為直角坐標方程可得
.極坐標方程化為直角坐標方程可得![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
(2)設![]() 的極坐標分別為
的極坐標分別為![]() ,則
,則![]() ,聯立極坐標方程可得
,聯立極坐標方程可得![]() , 則
, 則![]() ,結合三角函數的性質計算可得
,結合三角函數的性質計算可得![]() .
.
解法二: (1)同解法一
(2)曲線![]() 表示圓心為
表示圓心為![]() 且半徑為1的圓.聯立直線參數方程的標準形式與圓的方程可得
且半徑為1的圓.聯立直線參數方程的標準形式與圓的方程可得![]() ,結合參數的幾何意義知
,結合參數的幾何意義知![]() , 則
, 則![]()
解法三: (1)同解法一
(2)曲線![]() 表示圓心為
表示圓心為![]() 且半徑為1的圓.
且半徑為1的圓. ![]() 的普通方程為
的普通方程為![]() , 由弦長公式可得
, 由弦長公式可得![]() ,則
,則![]() 是等邊三角形,
是等邊三角形,![]() ,
, ![]() .
.
詳解:解法一:(1)由![]() 得
得![]() 的普通方程為
的普通方程為![]() ,
,
又因為![]() , 所以
, 所以![]() 的極坐標方程為
的極坐標方程為![]() .
.
由![]() 得
得![]() ,即
,即![]() ,
,
所以![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
(2)設![]() 的極坐標分別為
的極坐標分別為![]() ,則
,則![]()
由![]() 消去
消去![]() 得
得![]() ,
,
化為![]() ,即
,即![]() ,
,
因為![]() ,即
,即![]() ,所以
,所以![]() ,或
,或![]() ,
,
即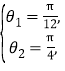 或
或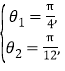 所以
所以![]() .
.
解法二: (1)同解法一
(2)曲線![]() 的方程可化為
的方程可化為![]() ,表示圓心為
,表示圓心為![]() 且半徑為1的圓.
且半徑為1的圓.
將![]() 的參數方程化為標準形式
的參數方程化為標準形式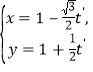 (其中
(其中![]() 為參數),代入
為參數),代入![]() 的直角坐標方程為
的直角坐標方程為![]() 得,
得,![]() ,
,
整理得,![]() ,解得
,解得![]() 或
或![]() .
.
設![]() 對應的參數分別為
對應的參數分別為![]() ,則
,則![]() .所以
.所以![]() ,
,
又因為![]() 是圓
是圓![]() 上的點,所以
上的點,所以![]()
解法三: (1)同解法一
(2)曲線![]() 的方程可化為
的方程可化為![]() ,表示圓心為
,表示圓心為![]() 且半徑為1的圓.
且半徑為1的圓.
又由①得![]() 的普通方程為
的普通方程為![]() ,
,
則點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
所以![]() ,所以
,所以![]() 是等邊三角形,所以
是等邊三角形,所以![]() ,
,
又因為![]() 是圓
是圓![]() 上的點,所以
上的點,所以![]() .
.


科目:高中數學 來源: 題型:
【題目】已知△ABC中, ![]() =λ
=λ ![]() (0<λ<1),cosC=
(0<λ<1),cosC= ![]() ,cos∠ADC=
,cos∠ADC= ![]() .
.
(1)若AC=5.BC=7,求AB的大小;
(2)若AC=7,BD=10,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為 ![]() (其中α為參數),以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=4sinθ.
(其中α為參數),以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=4sinθ.
(1)若A,B為曲線C1 , C2的公共點,求直線AB的斜率;
(2)若A,B分別為曲線C1 , C2上的動點,當|AB|取最大值時,求△AOB的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)為二次函數,且f(x-1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)當x∈[t,t+2],t∈R時,求函數f(x)的最小值(用t表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}的各項均為正數,且2a3是a2與a6的等比中項,2a1+3a2=16.
(1)求數列{an}的通項公式;
(2)設bn=log2a1+log2a2+…+log2an , 求數列{ ![]() }的前n項和Sn .
}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=a(x﹣lnx)+ ![]() ﹣
﹣ ![]() ,a∈R.
,a∈R.
(1)討論f(x)的單調性;
(2)當a= ![]() 時,證明:f(x)>f′(x)+
時,證明:f(x)>f′(x)+ ![]() 對于任意的x∈[1,2]成立.
對于任意的x∈[1,2]成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了解高一年級學生身高發育情況,對全校![]() 名高一年級學生按性別進行分層抽樣檢查,測得身高(單位:
名高一年級學生按性別進行分層抽樣檢查,測得身高(單位:![]() )頻數分布表如表
)頻數分布表如表![]() 、表
、表![]() .
.
表![]() :男生身高頻數分布表
:男生身高頻數分布表
身高/ |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
表![]() :女生身高頻數分布表
:女生身高頻數分布表
身高/ |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
(1)求該校高一女生的人數;
(2)估計該校學生身高在![]() 的概率;
的概率;
(3)以樣本頻率為概率,現從高一年級的男生和女生中分別選出![]() 人,設
人,設![]() 表示身高在
表示身高在![]() 學生的人數,求
學生的人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com