Question

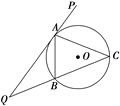
【題目】如圖所示，直線PQ與⊙O切于點A，AB是⊙O的弦，∠PAB的平分線AC交⊙O于點C，連接CB，并延長與直線PQ相交于Q點．

(1)求證：QC·AC＝QC2－QA2；

(2)若AQ＝6，AC＝5，求弦AB的長．

Answer 1

【答案】（1）見解析（2）

【解析】試題分析：（1）因為PQ與⊙O相切于點A，所以∠PAC＝∠CBA＝∠BAC，所以AC＝BC. 由割線定理得：QA2＝QB·QC＝(QC－BC)QC，所以QC·BC＝QC2－QA2，所以QC·AC＝QC2－QA2.（2）由條件，求出QC＝9，又△QAB∽△QCA，求出AB＝.

試題解析：

(1)證明：因為PQ與⊙O相切于點A，

所以∠PAC＝∠CBA，

因為∠PAC＝∠BAC，

所以∠BAC＝∠CBA，

所以AC＝BC.

由割線定理得：QA2＝QB·QC＝(QC－BC)QC，

所以QC·BC＝QC2－QA2，

所以QC·AC＝QC2－QA2.

(2)解：由AC＝BC＝5，AQ＝6及(1)知，QC＝9，

由∠QAB＝∠ACQ知△QAB∽△QCA，

所以＝，

所以AB＝.