
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)若![]() 為偶函數,求
為偶函數,求![]() 的值并寫出
的值并寫出![]() 的增區間;
的增區間;
(Ⅱ)若關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() ,當
,當![]() 時,求
時,求![]() 的最小值;
的最小值;
(Ⅲ)對任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求函數![]() 的極值;
的極值;
(3)若函數![]() 在區間
在區間![]() 上是增函數,試確定
上是增函數,試確定![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時, ![]() 恒成立,
恒成立, ![]() 不存在極值.當
不存在極值.當![]() 時,
時,
![]() 有極小值
有極小值![]() 無極大值.(3)
無極大值.(3)![]() .
.
【解析】試題分析:
(1)當![]() 時,求得
時,求得![]() ,得到
,得到![]() 的值,即可求解切線方程.
的值,即可求解切線方程.
(2)由定義域為![]() ,求得
,求得![]() ,分
,分![]() 和
和![]() 時分類討論得出函數的單調區間,即可求解函數的極值.
時分類討論得出函數的單調區間,即可求解函數的極值.
(3)根據題意![]() 在
在![]() 上遞增,得
上遞增,得![]() 對
對![]() 恒成立,進而求解實數
恒成立,進而求解實數![]() 的取值范圍.
的取值范圍.
試題解析:
(1)當![]() 時,
時, ![]() ,
, ![]() ,
,
![]() ,又
,又![]() ,∴切線方程為
,∴切線方程為![]() .
.
(2)定義域為![]() ,
, ![]() ,當
,當![]() 時,
時, ![]() 恒成立,
恒成立, ![]() 不存在極值.
不存在極值.
當![]() 時,令
時,令![]() ,得
,得![]() ,當
,當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,
,
所以當![]() 時,
時, ![]() 有極小值
有極小值![]() 無極大值.
無極大值.
(3)∵![]() 在
在![]() 上遞增,∴
上遞增,∴![]() 對
對![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() .
.
點睛:導數是研究函數的單調性、極值(最值)最有效的工具,而函數是高中數學中重要的知識點,所以在歷屆高考中,對導數的應用的考查都非常突出 ,本專題在高考中的命題方向及命題角度 從高考來看,對導數的應用的考查主要從以下幾個角度進行: (1)考查導數的幾何意義,往往與解析幾何、微積分相聯系. (2)利用導數求函數的單調區間,判斷單調性;已知單調性,求參數. (3)考查數形結合思想的應用.
【題型】解答題
【結束】
22
【題目】已知圓![]() :
: ![]() 和點
和點![]() ,
, ![]() 是圓
是圓![]() 上任意一點,線段
上任意一點,線段![]() 的垂直平分線和
的垂直平分線和![]() 相交于點
相交于點![]() ,
, ![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)點![]() 是曲線
是曲線![]() 與
與![]() 軸正半軸的交點,直線
軸正半軸的交點,直線![]() 交
交![]() 于
于![]() 、
、![]() 兩點,直線
兩點,直線![]() ,
, ![]() 的斜率分別是
的斜率分別是![]() ,
, ![]() ,若
,若![]() ,求:①
,求:①![]() 的值;②
的值;②![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應黨中央“扶貧攻堅”的號召,某單位指導一貧困村通過種植紫甘薯來提高經濟收入.紫甘薯對環境溫度要求較高,根據以往的經驗,隨著溫度的升高,其死亡株數成增長的趨勢.下表給出了2018年種植的一批試驗紫甘薯在不同溫度時6組死亡的株數:
溫度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡數 | 6 | 11 | 20 | 27 | 57 | 77 |
經計算:![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中![]() 分別為試驗數據中的溫度和死亡株數,
分別為試驗數據中的溫度和死亡株數,![]() .
.
(1)![]() 與
與![]() 是否有較強的線性相關性? 請計算相關系數
是否有較強的線性相關性? 請計算相關系數![]() (精確到
(精確到![]() )說明.
)說明.
(2)并求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() (
(![]() 和
和![]() 都精確到
都精確到![]() );
);
(3)用(2)中的線性回歸模型預測溫度為![]() 時該批紫甘薯死亡株數(結果取整數).
時該批紫甘薯死亡株數(結果取整數).
附:對于一組數據![]() ,
,![]() ,……,
,……,![]() ,
,
①線性相關系數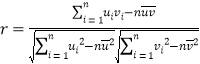 ,通常情況下當
,通常情況下當![]() 大于0.8時,認為兩
大于0.8時,認為兩
個變量有很強的線性相關性.
②其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
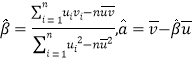 ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 同時滿足:①在定義域內存在
同時滿足:①在定義域內存在![]() ,使得
,使得![]() 成立;
成立;
②不等式![]() 的解集有且只有一個元素;數列
的解集有且只有一個元素;數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)求![]() 的表達式;
的表達式;
(Ⅱ)求數列![]() 的通項公式;
的通項公式;
(Ⅲ)設![]() ,
,![]() ,
,![]() 的前
的前![]() 項和為
項和為![]() ,若
,若![]() 對任意
對任意![]() ,且
,且![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
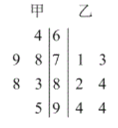
【題目】在桂林市某中學高中數學聯賽前的模擬測試中,得到甲、乙兩名學生的6次模擬測試成績(百分制)的莖葉圖.分數在85分或85分以上的記為優秀.
(1)根據莖葉圖讀取出乙學生6次成績的眾數,并求出乙學生的平均成績以及成績的中位數;
(2)若在甲學生的6次模擬測試成績中去掉成績最低的一次,在剩下5次中隨機選擇2次成績作為研究對象,求在選出的成績中至少有一次成績記為優秀的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平直角坐標系![]() 中,已知點
中,已知點![]() ,
,![]()
(1)在![]() 軸的正半軸上求一點
軸的正半軸上求一點![]() ,使得以
,使得以![]() 為直徑的圓過
為直徑的圓過![]() 點,并求該圓的方程;
點,并求該圓的方程;
(2)在(1)的條件下,點![]() 在線段
在線段![]() 內,且
內,且![]() 平分
平分![]() ,試求
,試求![]() 點的坐標.
點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩定點![]() ,
, ![]() 和一動點
和一動點![]() ,給出下列結論:
,給出下列結論:
①若![]() ,則點
,則點![]() 的軌跡是橢圓;
的軌跡是橢圓;
②若![]() ,則點
,則點![]() 的軌跡是雙曲線;
的軌跡是雙曲線;
③若![]() ,則點
,則點![]() 的軌跡是圓;
的軌跡是圓;
④若![]() ,則點
,則點![]() 的軌跡關于原點對稱;
的軌跡關于原點對稱;
⑤若直線![]() 與
與![]() 斜率之積等于
斜率之積等于![]() ,則點
,則點![]() 的軌跡是橢圓(除長軸兩端點).
的軌跡是橢圓(除長軸兩端點).
其中正確的是__________(填序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com